Responda os exercícios a seguir sobre geometria espacial e treine os seus conhecimentos sobre o assunto.
1) (PUC RS/2013) Um desafio matemático construído pelos alunos do Curso de Matemática tem as peças no formato de um cone. A figura abaixo representa a planificação de uma das peças construídas. A área dessa peça é de __ cm².
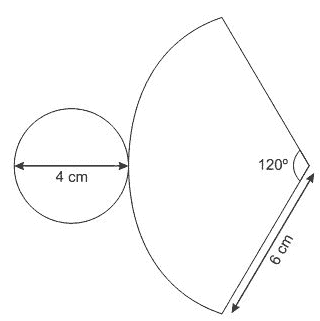
a) 10π
b) 16 π
c) 20 π
d) 28 π
e) 40 π
Ver resposta
A área da peça equivale à soma da área da base com a área lateral, pois se trata da planificação de um cone.
Assim, a área da base do cone é dada pela fórmula:
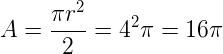
A área lateral é dada pela fórmula:
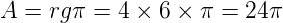
A área total do cone é a soma das áreas da base e lateral, assim:
At = 16π + 24π = 40π
Resposta D.
2) (UCS INV/2013) De uma caixa d’água de forma cúbica, cujas arestas medem 0,9 metros e contém água até a altura de 0,7 metros, devem ser retirados 162 litros de água.
Com essa retirada, a altura do nível de água irá baixar ____________, restando __________ de água na caixa.
Assinale a alternativa que preenche correta e respectivamente as lacunas acima. (dado 1 litro = 1 dm³)
a) 20 cm e 405 litros
b) 20 cm e 567 litros
c) 2 cm e 405 litros
d) 30 cm e 567 litros
e) 3 cm e 405 litros
Ver resposta
A caixa possui o formato de um cubo, onde largura = comprimento = altura = 0,9 m.
O problema diz que a caixa possui água até a altura 0,7 m. Assim, temos um volume de: V = 0,9 x 0,9 x 0,7 = 0,567 m³ de água.
No entanto, desse volume devem ser retirados 162 litros de água.
Como 1 litro = 0,001 m³.
Então:
162 x 0,001 = 0,162 m³
Agora precisamos retirar de 0,567 m³ de água 0,162 m³, logo:
0,567 m³ – 0,162 m³ = 0,405 m³ que é a quantidade de água restante após a retirada de 162 litros.
Precisamos calcular agora a nova altura da água na caixa.
Então:
Comprimento x Largura x Altura = Volume
0,9 m x 0,9 m x Altura = 0,162m³
0,81 m² x Altura = 0,162 m³
Altura = 0,162 / 0,81 = 0,2 m
Portanto, com a retirada de 162 litros a altura da água irá baixar 0,2 m ou 20 cm restando 0,405 m³, ou 405 litros de água na caixa.
3) (UFSM) Na figura, o perímetro do quadrilátero ABCD mede 4(1 + √2) cm. Então o volume do cubo em cm³, é
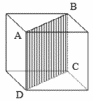
a) 4(1 +√2).
b) 8.
c) 16.
d) 64.
e) 2√3.
Ver resposta
A diagonal de um cubo é: d = a√2
Então, em ABCD temos dois lados medindo a e dois medindo a√2.
Assim, o perímetro é:
2a + 2a√2 = 2a(1 + √2)
Fazendo,
2a(1 + √2) = 4(1 + √2 ) ⇒
2a = 4 ⇒
a = 4/2 ⇒
a = 2
Dessa forma, podemos calcular o volume do cubo:
V = a³ = 2³ = 8 cm³
Resposta B.
4) Sabemos que o raio da Terra equivale a 6.371 km. Com essa informação, calcule a área superficial do planeta Terra.
Ver resposta
Como a Terra é uma esfera, então podemos utilizar a fórmula da esfera para calcular a área superficial de um objeto esférico:
A = 4πr² = 4 x 3,14159 x 6.371² = 510.064.041,1 km²
Portanto, a área superficial da Terra é de cerca de: 510.064.041,1 km²


