Conjuntos: União, Interseção e Diferença

Conjuntos como conhecemos são uma coleção ou grupos de objetos, ou símbolos aos quais chamamos de elementos.

Vamos estudar nesse artigo como funciona as relações de pertinência, inclusão, conjunto das partes, além das operações com conjuntos.

Notação e representação de conjuntos

Na prática a notação para conjuntos é usada letras do alfabeto em maiúsculo: A, B, C, …, Z. E a representação de um conjunto pode ser feita de diversas maneiras. Vamos ver cada uma delas adiante.

Exemplos:

• O conjunto de todos os alunos de uma sala (A);
• O conjunto musical (M);
• O conjunto dos números inteiros (Ζ);
• O conjunto dos números naturais (Ν).

Elementos de um conjunto

Elemento de um conjunto é qualquer coisa que pertença a um determinado conjunto. Além disso, os elementos devem ser listados entre um par de chaves.

Quando listamos os elementos de um conjunto, devemos separá-los por vírgula ou ponto e vírgula, de acordo com a necessidade.

Exemplos:

1. Considere A como o conjunto das vogais, então listamos assim: A = {a, e, i, o, u}
2. Considere B como o conjunto das cores primárias: B = {vermelho, azul e amarelo}

Quando um conjunto apresenta elementos infinitos, ou seja, que não é possível contabilizar todos os elementos, usamos a reticências (…) para indicar que o conjunto é infinito.

Exemplos:

1. Conjunto dos números naturais: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …}
2. Conjunto dos números inteiros: Z = {…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …}

Principais formas de representar um conjunto

As principais formas de representarmos um conjunto são:

Enumerar os elementos:

Exemplo: A = {a, e, i, o, u}

Através de uma propriedade que se repete:

Exemplo: B = {x ∈ A; x é vogal}, corresponde ao conjunto do exemplo anterior

Através do Diagrama de Venn:

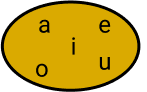
Na matemática também admite a existência do conjunto vazio, sem elemento, sendo representados por: {} ou ∅. E do conjunto unitário, que contém apenas um elemento.

Relação de pertinência

Pertinência é a característica associada a um elemento ao qual faz parte de um conjunto.

Quando queremos indicar que um elemento pertence a um conjunto, usamos o símbolo: ∈ (pertence).

Quando queremos indicar que um elemento não pertence a um determinado conjunto, usamos o símbolo: ∉ (não pertence).

Exemplos:

• 1 pertence ao conjunto dos números naturais (N): 1 ∈ N;
• João pertence ao conjunto dos alunos da sala: João ∈  A;
• 0,5 pertence ao conjunto dos números reais: 0,5 ∈ R;
• 11 pertence ao conjunto dos números primos: 11 ∈ P;
• b não pertence ao conjuntos das vogais A: b ∉ A.

Relação de inclusão

A relação de inclusão pode ser bastante confundida se o aluno não entender a simbologia:

• Quando falamos que o conjunto A está contido no conjunto B, então todo elemento de A pertence a B e usamos o símbolo: A ⊂ B;
• Quando falamos que B contém A, usamos o símbolo: B ⊃ A
• Quando falamos que o conjunto A não está contido em B, usamo o símbolo: A ⊄ B;
• Quando falamos que o conjunto B não contém A, usamos o símbolo: B ⊅ A;
• Quanto falamos que o conjunto A é subconjunto de B, ou seja, que todos os elementos de A também são elementos de B, usamos o símbolo: A ⊆ B;
• Por fim, quando dizemos que B não é subconjunto de A, ou seja, B não está contido nem é igual a A, usamos o símbolo: B ⊈ A.

Importante: a simbologia para relação de inclusão deve ser usada para relacionar conjuntos, se usar para relacionar elementos está errado.

Exemplos:

• Forma errada:
  • 1 ⊂ {1, 2, 3, 4, 5}; 1 neste caso é um elemento, para ser conjunto deveria está entre chaves, o símbolo ⊂ deve ser usado para relacionar conjuntos;
  • {1} ∈ {1, 2, 3, 4, 5}; {1} neste caso é um conjunto, o símbolo ∈ serve para relacionar elementos;
• Forma correta:
  • {1} ⊂ {1, 2, 3, 4, 5};
  • {1} ⊄ {{1}, 2, 3, 4, 5}; aqui {1} é elemento e não conjunto. Então: {1} ∈ {{1}, 2, 3, 4, 5} .

Representação gráfica pelo Diagrama de Venn

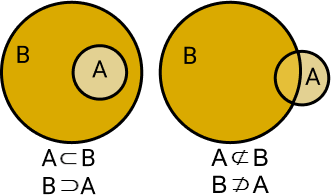
Subconjuntos

Dado um conjunto A, dizemos que B é um subconjunto de A, se B estiver contido em A, denotado por: B ⊂ A (B está contido em A). É o mesmo que dizer que B está dentro de A, ou seja, se todos os elementos de B estão dentro de A.

Exemplos:

Diagrama de Venn:  

Perceba que o conjunto B está literalmente dentro de A, portanto é subconjunto de A. Os elementos de B também são elementos de A.

C = {a, e, i, o, u} e D = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z}

O conjunto das vogais C é subconjunto do conjunto do alfabeto da língua portuguesa D. Ou seja, o conjunto das vogais está contido no conjunto do alfabeto D.

Considerando que A e B são conjuntos, dizemos que A ⊂ B e B ⊂ A se, e somente se, A = B.

Exemplos:

Diagrama de Venn

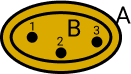
Os elementos de A são os mesmo elementos de B.

A = {1, 2, 3} e B = {3, 2, 1}; a ordem dos elementos não importa, os dois conjuntos tem os mesmo elementos.

Observações:

• Todo conjunto é subconjunto de si mesmo, pois todos os seus elementos são elementos dele mesmo;
• O conjunto vazio é subconjunto de qualquer conjunto.

Conjunto unitário

Dizemos que um conjunto é unitário quando tem somente um elemento.

Exemplos:

• A = {a}
• B = {10}

Conjunto universo

Chamamos de conjunto universo um conjunto que contém todos os elementos dos conjuntos que estamos representando. Esse conjunto é simbolizado pela letra maiúscula U.

Exemplo:

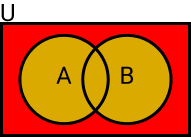
O conjunto U é o conjunto universo dos conjuntos A e B.

Complementar

Conjunto complementar é aquele que contém todos os elementos do conjunto universo que não estão no outro conjunto.

Definição do conjunto complementar

Seja A um conjunto, temos que o conjunto complementar A^C é definido por:

A^C = U – A = {x | x ∈ U e X ∉ A}

Exemplo:

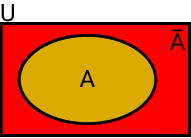
O conjunto complementar de A são todos os elementos que estão no conjunto universo U (em vermelho, mas não estão em A).

É simbolizado pela letra do conjunto que queremos encontrar o complementar com um traço em cima. Símbolos usados para conjunto complementar: Ä, A^C, A’, C_UA ou

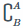
Conjuntos das partes

Seja A um conjunto qualquer, chamamos de conjunto das partes de A todos os subconjuntos possíveis da conjunto A. É representado por P(A).

Exemplos: A = {1, 2, 3}

Como determinar o conjunto das partes?

Para determinar o conjunto das partes para A, temos que escrever todos os subconjuntos de A.

• Sabemos que o conjunto vazio é subconjunto de qualquer conjunto: ∅;
• Devemos considerar em A os subconjuntos com um elemento: {1}, {2}, {3};
• Agora subconjuntos com dois elementos: {1, 2}, {1, 3}, {2, 3};
• Consideremos agora o subconjunto com três elementos: {1, 2, 3};
• Então, por fim, temos o conjunto das partes para A: P(A) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.

Esse passo ajuda você, caro leitor, a entender como funciona o conjunto das partes. No entanto, um conjunto com muitos elementos pode necessitar de mais combinações de elementos.

Número de elementos do conjunto das partes

Para saber a quantidade de elementos do conjunto das partes e, portanto, saber a quantidade de subconjuntos de um conjunto qualquer, utilizamos a seguinte fórmula:

Seja A um conjunto qualquer, então:

O número de elementos do conjunto das partes de A: n[P(A)] = 2^n(A), onde n(A) é a quantidade de elementos de A.

Exemplo:

• A = {1, 2, 3}; então: n[P(A)] = 2³ = 8

Pelo exemplo anterior, percebemos que o conjunto das partes para o conjunto A tem exatamente 8 elementos.

Igualdade de conjuntos

Sejam os conjuntos A e B, temos que A = B se, e somente se, eles possuem os mesmos elementos. Independente da ordem como são apresentados ou da quantidade.

Exemplos:

• A = {1, 2, 3} e B = {3, 2, 1}
• A = {1, 2, 3, 3, 3, 3} e B = {1, 2, 3}

Temos que A = B nos dois exemplos acima.

Leis de De Morgan

As leis de De Morgan mostram que:

1. O complementar da união de dois conjuntos é igual à interseção dos complementares dos dois conjuntos;
2. O complementar da interseção de dois conjuntos é igual à união dos complementares dos dois conjuntos.

Exemplos:

Podemos verificar através do Diagrama de Venn:

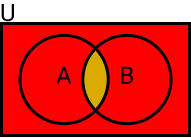
• (A ∪ B)^C = A^C ∩ B^C

• (A ∩ B)^C = A^C ∪ B^C

Operações com conjuntos

União

Em muitos problemas em provas de vestibulares e do ENEM é necessário saber as operações com conjuntos. São elas: União, Interseção e Diferença.

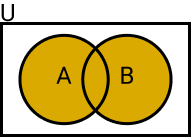
A união de dois conjuntos no conjunto universo U é formada pelos elementos que pertencem a A ou B.

• A ∪ B (Leia-se: A união B)

Definição de união

Sejam A e B conjuntos, a união de A com B é dada por:

• A ∪ B = {x ∈ U | x ∈ A ou x ∈ B}

Propriedades

• A ∪ B = B ∪ A
• B ⊂ A ⇒ A ∪ B = A
• A ∪ ∅ = A
• (A ∪ B) ∪ C = A ∪ (B ∪ C) = A ∪ B ∪ C

Exemplos:

• {1, 2, 3} ∪ {4, 5} = {1, 2, 3, 4, 5}
• {a, b, c, c, c} ∪ {d} = {a, b, c, d}
• {1, 2} ∪ ∅ = {1, 2}

Interseção

A interseção de dois conjuntos no conjunto universo U é formada pelos elementos que pertencem a A e B.

• A ∩ B (Leia-se: A interseção B)

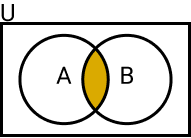
Definição de interseção

Sejam A e B conjuntos, a interseção de A com B é dada por:

• A ∩ B = {x ∈ U | x ∈ A e x ∈ B}

Exemplos:

• {1, 2, 3, 4, 5} ∩ {5, 6, 7} = {5}
• {a, b, c} ∩ {b, c, d} = {b, c}
• {1, 2} ∩ ∅ = ∅

Propriedades

• A ∩ B = B ∩ A
• B ⊂ A ⇔ A ∩ B = B
• A ∩ ∅ = ∅
• (A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C
• (A ∩ B) ⊂ (A ∪ B)

Diferença

A diferença de dois conjuntos no conjunto universo U é formada pelos elementos que pertencem a A, mas não pertencem a B.

• A – B (Leia-se: a diferença entre A e B)

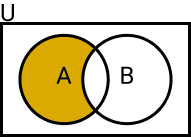
Definição da diferença

Sejam A e B conjuntos, a diferença entre A e B é dada por:

• A − B = {x ∈ U | x ∈ A e x ∉ B}

Exemplos:

• A = {1, 2, 3, 4} e B = {1, 4, 6}
• B – A = {6}
• A – B = {2, 3}

Propriedades

• (A – B) ⊂ A
• A – ∅ = A
• ∅ – A = ∅
• A – (A ∩ B) = A – B

Exercícios

Os exercícios sobre conjuntos estão disponíveis acessando o link a seguir:

• Exercícios sobre operações com conjuntos

Leia também…

• Razão e Proporção
• Subtração de Frações
• Números Primos
• Regra de Três Composta
• Critérios de Divisibilidade
• Porcentagem
• Tabuada
• Conjuntos Numéricos