O círculo trigonométrico é uma circunferência com um raio unitário. Nessa circunferência fixamos um ponto que chamaremos de A, onde esse ponto será a origem dos arcos e adotaremos o sentido anti-horário como positivo.
Quadrantes do Círculo Trigonométrico
O círculo trigonométrico é dividido em 4 partes, chamadas de quadrantes:
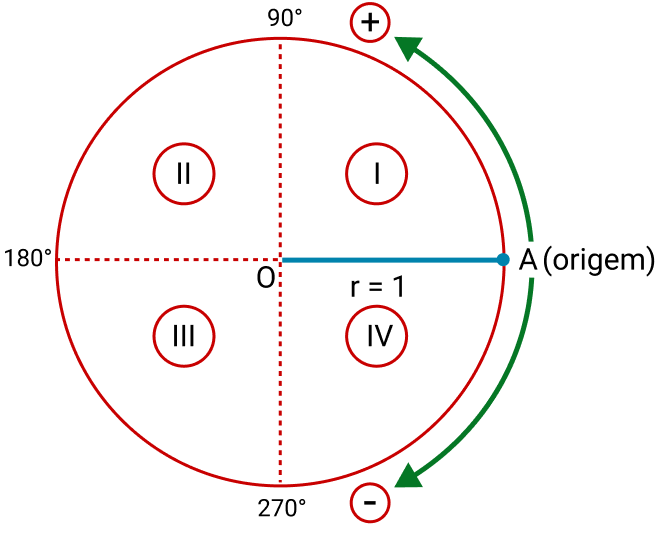
São eles:
- I: primeiro quadrante 0° a 90°;
- II: segundo quadrante 90° a 180°;
- III: terceiro quadrante, 180° a 270° ;
- IV: quarto quadrante 270° a 360° ;
- O: centro do círculo.
Arco e Circunferência
Em uma circunferência, dois pontos A e B dividem-na em duas partes. Essa divisão chamamos de arcos, sendo A e B as extremidades desse arco que simbolizaremos da seguinte maneira:

A parte em vermelho, entre A e B, é o que chamamos de arco.
Ângulo Central
Considere a circunferência C abaixo. Chamamos de ângulo central em C, um ângulo coplanar, cujo vértice é o centro de C, esse ângulo é denominado o ângulo central relativo a C.
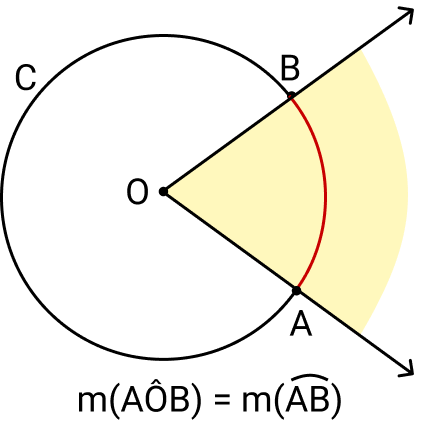
A parte em vermelho, entre os pontos A e B, é o arco da circunferência contido num ângulo central, e é chamado de o arco correspondente a este ângulo.
Medidas de Ângulos e Arcos
Podemos medir ângulos e arcos de duas maneiras distintas: em graus e em radianos.
Medidas em Graus
Uma circunferência é dividida em 360 partes iguais entre si, cada uma dessas partes corresponde a um arco de 1º.
Um arco de 1º, dividido em 60 partes iguais entre si, cada uma dessas partes (arcos) corresponde a um minuto (1’).
Da mesma maneira, se dividirmos um arco de 1 minuto em 60 partes iguais entre si, cada uma dessas partes mede um segundo (1”).
Portanto, 1° = 60’ e 1’ = 60”
Um arco de circunferência com medidas a graus, b minutos e c segundos, então a°b’c”.
Medidas em Radianos
A medida de um arco, em radiano, é a razão entre o comprimento do arco e o raio da circunferência onde o arco está determinando. Radiano é simbolizado por rad.
Exemplo:
Seja a medida de um ângulo α, em radianos, cujo arco tem comprimento l que estão contidos numa circunferência com raio r, então:

Ou seja, a medida do ângulo α é o comprimento do arco definido como l sobre o comprimento do raio r.
As medidas de arcos em uma circunferência em graus e radianos são diretamente proporcionais, dessa forma podemos converter uma média em outra através de uma regra de três simples.
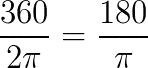
Logo, se quisermos converter uma medida em graus para radianos, por exemplo, devemos proceder da seguinte forma:
Graus Radianos
a ——————– α
180
—————— π
Onde:
- α é a medida do ângulo em radianos;
- a é a medida do ângulo em graus;
Para isso, deve-se utilizar a seguinte fórmula:
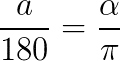
A conversão é feita multiplicando em cruz.
Arco Orientado
Nas circunferências em trigonometria é adotado o percurso no sentido anti-horário como positivo e o sentido horário como negativo.
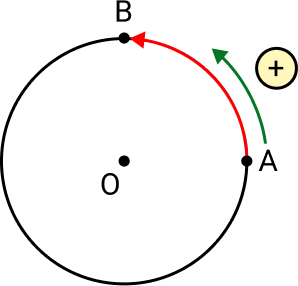
Exemplos:
Arco orientado de A a B, com centro O, e medidas π/2 ou 90°.
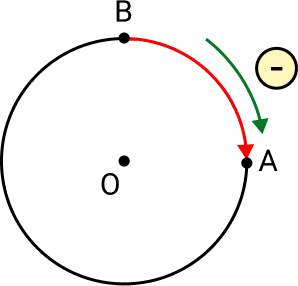
Arco orientado de B a A, com centro O, e medidas -π/2 ou -90°.
Círculo Trigonométrico
Toda circunferência orientada, com centro O e raio unitário, em que podemos escolher um ponto de origem para os arcos, é chamada de circunferência trigonométrica ou círculo trigonométrico.
Os arcos em um círculo trigonométrico tem as mesmas medidas absolutas α igual ao comprimento l, pois α = l/r e r = 1.
Como construir um Círculo Trigonométrico?
Para construir um círculo trigonométrico precisamos escolher o sentido anti-horário ou horário, devemos seguir os passos:
Sentido Anti-Horário: escolha um ponto A, inicial, percorrendo no sentido anti-horário, um arco de comprimento π/5, assim obtemos um arco de π/5.

Sentido Horário: escolha um ponto A, inicial, percorrendo no sentido horário, obtemos um arco de comprimento 2, assim teremos um arco -2.
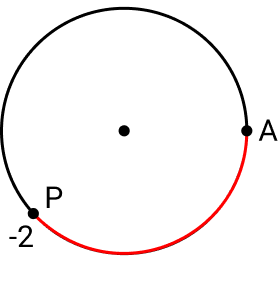
Seguindo esses passos, chegaremos a um círculo trigonométrico, que pode ser em radianos (rad) ou em graus (°).
Com o círculo trigonométrico, você pode obter, sem precisar fazer a conversão, a medida para um ângulo em grau ou radiano. Veja abaixo os dois círculos com as medidas dos ângulos em graus e em radianos.
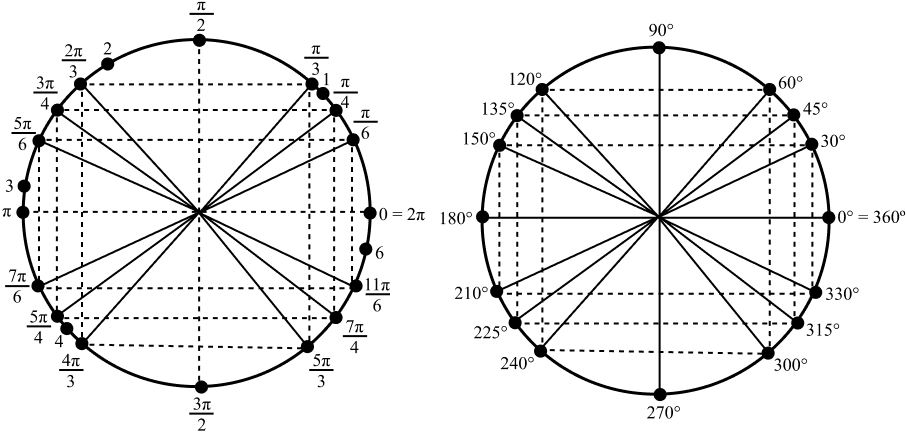
Perceba que alguns ângulos no círculo acima são simétricos. Nesse caso, apenas alguns ângulos foram colocados na imagem acima para exemplificar. Pode ter muito mais.
Com o círculo trigonométrico, o estudo das razões trigonométricas fica muito mais simples de visualizar. Desenhando um triângulo, podemos ver como são definidas as relações trigonométricas.

Exercícios de trigonometria
Acesse os exercícios no link abaixo:
Bons estudos!
Leia mais…



