Relações trigonométricas são funções trigonométricas relacionadas com os lados e o ângulo de um triângulo retângulo.
As funções seno e cosseno de um ângulo são as funções trigonométricas básicas e as mais conhecidas, através delas é possível chegar em outras funções trigonométricas: tangente (tg), cotangente (cot), secante (sec) e cossecante (csc).
Exemplo:
Seja o triângulo ABC abaixo, em que θ representa o ângulo:
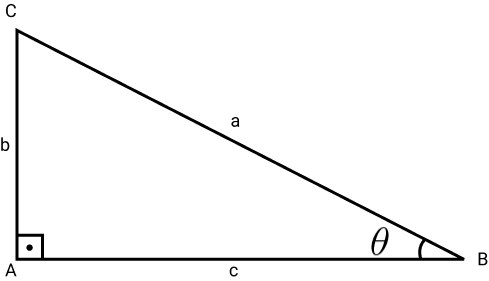
Veja como podemos representar as relações trigonométricas a partir das funções seno, cosseno e tangente.
- A função seno é representado como sen(θ);
- A função cosseno é representado por cos(θ);
- A função tangente é representada por tan(θ).
Essas funções são definidas pela razão entre os lados do triângulo e o ângulo θ. Assim:
- sen(θ) = b/a
- cos(θ) = c/a
- tan(θ) = b/c
Onde:
- a é a hipotenusa;
- b é o cateto oposto;
- c é o cateto adjacente ao ângulo θ.
Essas funções também são chamadas razões trigonométricas, pois é através das razões entre os lados que elas são obtidas.
A partir dessas razões podemos definir outras funções importantes na trigonometria: cotangente (cot), secante (sec) e cossecante (csc).
A tangente também pode ser representada como:
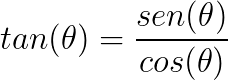
A cotangente é o inverso da tangente, logo:
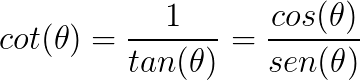
A secante é o inverso do cosseno:
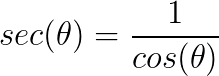
A cossecante é o inverso do seno:
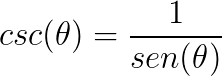
Perceba que encontramos as outras funções apenas conhecendo as funções seno e cosseno. Dessa forma,
- a tangente é o seno sobre o cosseno do ângulo;
- a cotangente é o inverso da tangente, ou seja, o cosseno sobre o seno do ângulo;
- a secante é o inverso do cosseno do ângulo;
- e a cossecante é o inverso do seno do ângulo.
Relações trigonométricas derivadas
Tendo conhecimento das relações trigonométricas básicas apresentadas no exemplo anterior, podemos derivar outras relações trigonométricas.
Exemplo:
Seja a relação fundamental sen²(θ) + cos²(θ) = 1
Se dividirmos toda a função por cos²(θ) temos:
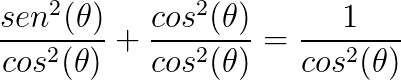
Sabemos, porém, pelo exemplo acima, que
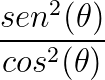
é a tangente ao quadrado e
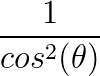
é a secante ao quadrado.
Assim, temos que:
- tan²(θ) + 1 = sec²(θ) ou sec²(θ) = 1 + tan²(θ)
Se dividirmos por sen²(θ) temos:
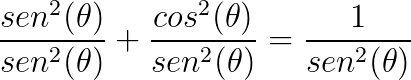
Sabemos que
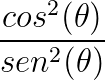
é a cotangente ao quadrado e
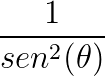
é a cossecante ao quadrado.
Substituindo, temos:
- 1 + cot²(θ) = csc²(θ) ou csc²(θ) = 1 + cot²(θ)
Identidades trigonométricas
Conheça agora algumas identidades trigonométricas que podem servir para a resolução de problemas envolvendo trigonometria.

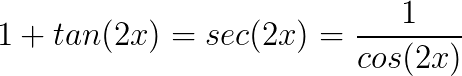
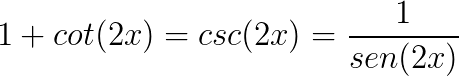
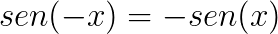
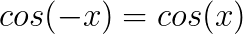
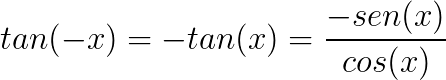
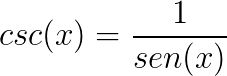
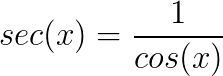
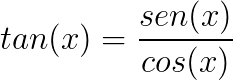
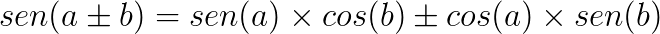
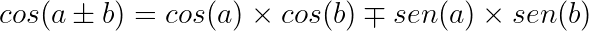
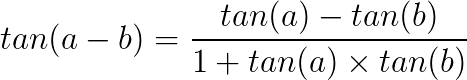
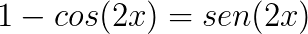
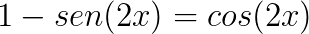
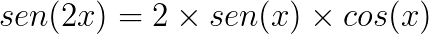
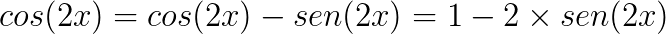
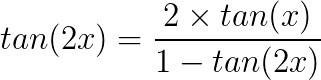
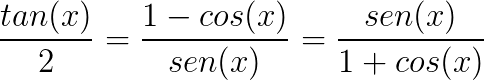
Bons estudos!
Leia mais…
Exercícios de trigonometria
Veja os exercícios acessando o link a seguir:



