A área do paralelogramo é a medida equivalente à superfície do paralelogramo. Paralelogramos são polígonos quadriláteros em que os lados opostos são paralelos e congruentes (mesma medida).

Os ângulos opostos e internos do paralelogramo também possuem as mesmas medidas pelo fato dos lados opostos serem paralelos. A soma dos ângulos internos é igual a 360°. Analogamente, a soma dos ângulos externos também é igual a 360°.
Para calcular a área de qualquer figura geométrica utilizamos a unidade de medida do Sistema Internacional para a área, que é a metro quadrado (m²). Podemos ainda utilizar variações como o centímetro quadrado (cm²), milímetro quadrado (mm²), etc.
Elementos do Paralelogramo
Todo paralelogramo possuem os seguintes elementos na sua formação:
- Quatro lados: possuem quatro lados, sendo os lados opostos paralelos. Os lados são segmentos de retas, também chamados de arestas, que se unem nos vértices;
- Quatro vértices: os vértices são pontos onde os lados se unem;
- Quatro ângulos internos: possui também quatro ângulos internos e os ângulos opostos são congruentes (mesma medida). Alguns paralelogramos, como o quadrado e o retângulo, possuem todos os ângulos congruentes;
- Quatro ângulos externos: todo paralelogramo possui ângulos externos que são complementares aos ângulos internos. A soma do ângulo complementar com o ângulo interno é igual a 180°;
- Duas diagonais: as diagonais do paralelogramo são segmentos de retas que ligam dois vértices opostos.
Exemplos de Paralelogramos
Os polígonos que são paralelogramos são:
- Retângulo: o retângulo é um paralelogramo, ele possui quatro lados paralelos. Os lados opostos possuem as mesmas medidas. Todos os ângulos são retos (90°);
- Quadrado: o quadrado também é um paralelogramo, tem as mesmas características do retângulo, a única diferença é que a medida de todos os lados e as diagonais são iguais.
- Losango: o losango é outro polígono que também é um paralelogramo, com lados opostos paralelos e congruentes. Além disso, os ângulos opostos possuem as mesmas medidas.
Leitura recomendada:
Cálculo da Área do Paralelogramo
O cálculo da área do paralelogramo é feito realizando o produto entre a base do polígono pela altura. Para isso utilizamos a seguinte fórmula:
- A = b . h
Onde:
- A: é a área;
- b: é a base;
- h: é a altura.
Leitura recomendada:
A área do quadrado pode utilizar a fórmula acima, veja o artigo sobre a área do quadrado para entender melhor.
A área do losango é diferente da fórmula acima mostrada, veja como calcular a área do losango.
Perímetro do Paralelogramo
O perímetro de um paralelogramo é a soma das medidas de todos os lados do polígono. Para calcular o perímetro, utilizamos a seguinte fórmula:
- P = 2(a + b)
- P: é o perímetro;
- a e b: são as medidas dos lados;
Leitura recomendada:
Diagonais do Paralelogramo
Todo paralelogramo possui duas digonais que dividem o polígono em duas partes cada diagonal.
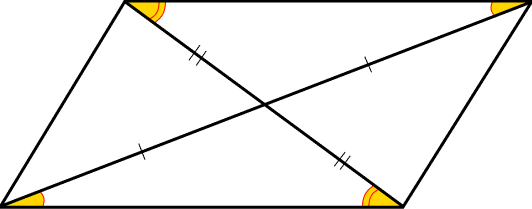
As diagonais se cruzam nos seus pontos médios, dessa forma o ponto de intersecção das diagonais é o centro do paralelogramo.
Exercício Resolvido
- Seja um paralelogramo ABCD com 30 cm de base e
10 cm de altura. Calcule a área desse polígono.
- Dados do problema:
- Base (b): 30 cm
- Altura (h): 10 cm
- Dados do problema:
- Área do Paralelogramo: a área é calculada pela seguinte fórmula: A = b .
h
- Substituindo os valores na fórmula, temos:
- A = 30 . 10 = 300 cm²
- Substituindo os valores na fórmula, temos:
Exercícios Propostos
Acesse os exercícios no link a seguir:



