Expressões Algébricas: Classificação e Operações

As expressões algébricas são expressões que envolvem variáveis e números com operações da aritmética. As variáveis podem assumir qualquer valor numérico.

Diferentemente das expressões numéricas, expressões envolvendo números e operações da aritmética, as algébricas vão um pouco além, representam também os valores desconhecidos.

As letras são chamadas de incógnitas, que são os números que não conhecemos. A representação dessas incógnitas é de responsabilidade da álgebra, por isso as expressões envolvendo incógnitas são chamadas de expressões algébricas.

Cálculo de uma Expressão Algébrica

Para realizar um cálculo de uma expressão algébrica com variáveis, devemos atribuir os valores dados no problema a essas variáveis.

Nos problemas específicos, os valores devem ser dados para a resolução.

Exemplo:

Para calcular a área de um retângulo temos a seguinte fórmula:

A = b . h

As variáveis b, que representa a base, e h, que representa a altura, devem ser substituídas por valores numéricos dados no problema.

Por exemplo, se um retângulo mede 10 cm de base e 5 cm de altura, substituindo os valores nas variáveis da fórmula, temos:

A = b . h = 10 . 5 = 50 cm²

Classificação das Expressões Algébricas

As expressões algébricas são classificadas em dois grupos: monômios e polinômios.

Monômios

Monômio é o nome dado a expressões que apresentam apenas o produto entre coeficientes (parte numérica) pelas variáveis (parte literal).

Exemplos:

1. 3xy: monômio onde o número 3 (coeficiente) multiplica as variáveis x e y (parte literal);
2. 5x²yz²: monômio com o coeficiente 5 e a parte literal x²yz²;
3. x: monômio com coeficiente 1 e parte literal x, apesar de o número 1 não aparecer, em toda variável podemos considerar a existência de um produto por 1, pois ele é neutro na multiplicação;
4. 10: monômio com coeficiente 10 e parte literal x⁰, pois x⁰ é 1, e 10 vezes 1 é 10.

Polinômios

Os polinômios são a adição e subtração de dois ou mais monômios, o prefixo poli que dizer muitos.

Exemplos:

• Adição: 3x + 2y + 3z
• Subtração: 2x²y – 3y – 2z
• Adição e Subtração: 3x³y²z – 2x²y + 4xyz² – xyz

Operações Algébricas

Podemos realizar operações algébricas entre polinômios e monômios usando as operações básicas da aritmética.

Soma e Subtração de Monômios

Podemos somar ou subtrair monômios quando eles têm a parte literal em comum. Então, procederemos da seguinte forma:

• Somamos ou subtraímos os coeficientes e mantemos a parte literal.

Exemplo:

• 3xy + 3xy² + 9xy – 3x²y + 2xy² = (3 + 9)xy + (3 + 2)xy² – 3x²y = 12xy + 5xy² – 3x²y

Multiplicação e Divisão de Monômios

Para multiplicar monômios, multiplicamos os coeficientes, primeiramente, e depois as incógnitas, tomando cuidado com as potências.

Exemplo:

• 3xy² . 4xy = (3 . 4).(x . x) . (y² . y) = 12 . x^{1 + 1} . y^{2 + 1} = 12x²y³

As potências de mesma base, na multiplicação, devem ser conservadas e depois somam-se os expoentes.

Para dividir dois monômios devemos dividir os coeficientes entre si e a parte literal também entre elas. Tomando cuidado ao dividir potências. Use as propriedades de potenciação: bases iguais, conserva a base e subtrai os expoentes.

Exemplo:

• 10x⁴ ÷ 2x = (10 ÷ 2) e (x⁴ ÷ x) = 5x³
• 16x ÷ 4x = (16 ÷ 4) e (x ÷ x) = 4

Soma e Subtração de Polinômios

Os polinômios são somados ou subtraídos colocando os termos comuns de mesma parte literal, juntos. Somente podemos somar ou subtrair os coeficientes em que a parte literal é comum, se for diferente não deve ser somada ou subtraída e, sim, conservada no resultado.

Exemplo:

• 2x² + 3y² – 5x + 3x + 2y² – 3xy = 2x² + (3 + 2)y² + (-5 + 3)x -3xy = 2x² + 5y² + 2x – 3xy
• 3x³ – 2x² + 3x² – 5x³ = (3 – 5)x³ + (-2 + 3)x² = -2x³ + x²

Multiplicação de Polinômios

Polinômios são multiplicados utilizando a propriedade distributiva da multiplicação.

• Multiplicar o primeiro termo do primeiro polinômio por todos os termos do segundo, multiplicar o segundo termo do primeiro polinômio por todos os termos do segundo, e assim por diante.

Exemplo:

• (3x + 2y) . (x + 2y) = (3x . x) + (3x . 2y) + (2y . x) + (2y . 2y) = 3x² + 6xy + 2xy + 2y²

Divisão de Polinômios

Para dividir dois polinômios devemos dividir os coeficientes entre si e a parte literal entre elas, tomando cuidado ao dividir as potência e usar as regras de divisão de potência: bases iguais, repete a base e subtrai os expoentes.

Exemplo:

Divisão de polinômio por monômio

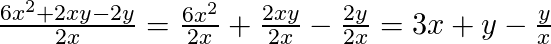
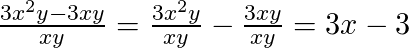
Divisão de polinômio por polinômio

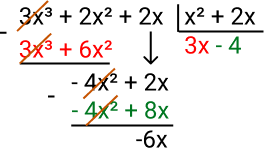
Simplificação de Expressões Algébricas

A simplificação de uma expressão algébrica ocorre pelas operações da aritmética adição e subtração. Consiste em pegar os termos semelhantes e somar ou subtrair para tornar a expressão mais simples e fácil de operar.

A simplificação acontece conservando as variáveis (parte literal) e somando ou subtraindo os coeficientes (números).

Exemplo:

Considere as seguintes expressões algébricas:

1. 2xy + 4x²y – xy + 3x²y
   • Simplificando: (2xy – xy) + (3x²y + 4x²y) = xy + 7x²y
   • Conservamos as variáveis e somamos ou subtraímos os números, assim: (2 – 1)xy + (3 + 4)x²y = 1xy + 7x²y = xy + 7x²y
2. 4ab + 5ab² + 8ab – 3ab² + 2ab – ab
   • Simplificando: devemos separar os termos positivos e semelhantes, assim:
   • (4ab + 8ab + 2ab – ab) + (- 3ab² + 5ab²) = (4 + 8 + 2 – 1)ab + (- 3 + 5)ab² = 13ab + 2ab²
   • Agrupamos os termos com grau 2 (ab²) e com grau 1 (ab), depois separamos os coeficientes (números) da parte literal (variáveis) para facilitar o cálculo.

Fatoração de Expressões Algébricas

A fatoração de uma expressão algébrica é reescrever a expressão de forma que coloquemos a parte comum como um produto da parte diferente.

Dessa forma, podemos fatorar expressões algébricas utilizando os seguintes casos:

• Fator comum: Quando temos uma variável em comum, coloquemos ela em evidência, isto é, coloquemos ela como um produto dos termos que não são comuns:
  • Exemplo: ax + bx = x . (a + b)

• Agrupamento: Quando temos vários termos e variáveis em comum, agrupamos eles para simplificar, colocando os grupos como um produto pelas variáveis que os multiplicam:
  • Exemplo: ax + bx + ay + by = x . (a + b) + y . (a + b) = (x + y) . (a + b)

• Trinômio Quadrado Perfeito: trinômio formado por três monômios que não possuem termos em comum. Utilizando adição:
  • Exemplo: a² + 2ab + b² = (a + b)²

• Trinômio Quadrado Perfeito: utilizando subtração de três monômios diferentes:
  • Exemplo: a² – 2ab + b² = (a – b)²

• Diferença de dois quadrados: quando temos dois termos em comum, de forma que os termos sejam um produto de uma soma por uma subtração:
  • Exemplo: (a + b) . (a – b) = a² – b²

• Cubo Perfeito (adição): quando temos a primeira parcela ao cubo (a³), mais o triplo de a²b (3a²b), mais o triplo de ab² (3ab²), mais o cubo de b (b³). Isto é igual ao cubo da soma de a mais b(a + b)³:
  • Exemplo: a³ + 3a²b + 3ab² + b³ = (a + b)³

• Cubo Perfeito (subtração): quando temos a primeira parcela ao cubo (a³), menos o triplo de a²b (3a²b), mais o triplo de ab² (3ab²), menos o cubo de b (b³). Isto é igual ao cubo da diferença entre a e b(a – b)³:
  • Exemplo: a³ – 3a²b + 3ab² – b³ = (a – b)³

Exercícios

• Exercícios de expressões algébricas