A divisão de polinômios de dois polinômios A(x) e B(x) não nulos, obtém um polinômio Q(x) e R(x) de forma que:
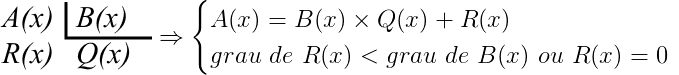
Onde:
- A(x): é o dividendo;
- B(x): é o divisor;
- Q(x): é o quociente;
- R(x): é o resto.
Vamos demonstrar aqui o método conhecido como método da chave.
Como Dividir Polinômios por Monômio?
Um polinômio é formado por vários monômios. Para dividir um polinômio por um monômio devemos proceder da seguinte forma:
Exemplo:
Seja o polinômio P(x) = 3x² + 2x + 2 e o monômio x. Primeiro devemos armar o problema para a divisão:
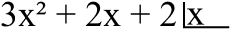
Depois devemos pegar o monômio 3x² do primeiro polinômio e dividir por x. Resulta em 3x, multiplicamos 3x por x e colocamos o resultado embaixo do número que dividimos com o sinal trocado. Então fazemos a soma. Como mostra a imagem:
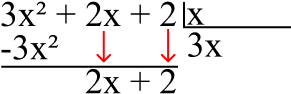
Continuamos o processo de divisão como no passo anterior:
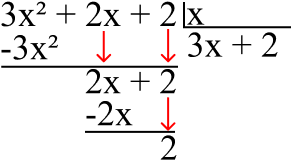
A divisão termina quando o grau do resto for menor que o grau do quociente. Assim, a divisão do polinômio 3x² + 2x + 2 pelo monômio x, resulta no polinômio 3x + 2.
Como Dividir Polinômios por Polinômios?
Agora vamos mostrar o processo de divisão de polinômios por polinômios.
Exemplo:
Considere os polinômios A(x) = 3x³ + 2x² + 2x – 1 e B(x) = x² + x + 2. Efetue a divisão de A(x) por B(x).
Primeiramente, temos que verificar o grau do dividendo para ver se é maior ou igual ao grau do divisor. Caso contrário, não será possível efetuar a divisão. No exemplo, o grau de A(x) = 3 e B(x) = 2. Vamos prosseguir.
Vamos armar o problema:
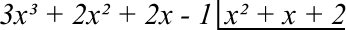
Então, devemos dividir o primeiro termo do dividendo com o primeiro do divisor, 3x³ dividido por x²:
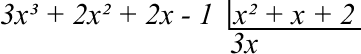
Agora multiplicamos o resultado (3x) por todo o divisor (x² + x + 2) começando da direita para a esquerda. O resultado deve ser colocado abaixo de cada termo coincidente do dividendo com o sinal trocado. Por fim, realize a soma.
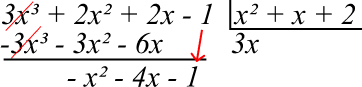
Agora, devemos dividir o resultado da soma anterior pelo divisor. Sempre pegando o maior termo do dividendo e dividindo pelo maior termo do divisor. Colocando o resultado embaixo de cada termo coincidente do dividendo.
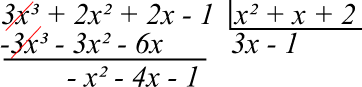
Devemos repetir o processo até que o grau do resto R(x) for menor que o grau do divisor B(x) ou o grau do resto R(x) for igual a zero.
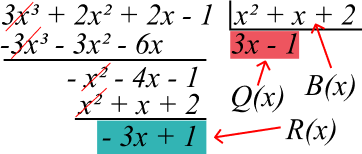
Como o grau de R(x) é menor que o grau de B(x), o processo de divisão se encerra. Então, a divisão do polinômio A(x) = 3x³ + 2x² + 2x – 1 pelo polinômio B(x) = x² + x + 2 resulta no polinômio Q(x) = 3x – 1.
Exercícios
Acesse os exercícios no link abaixo:



