Polinômios: Definição, Grau e Operações

Polinômios são expressões algébricas formados conforme a seguinte expressão:

• P(x) = a_nxⁿ + a_{n – 1}x^{n – 1} + … + a₁x + a₀

Além disso, um polinômio é formado por letras, chamada parte literal, e números, chamados coeficientes.

Exemplo:

• 2x² + 3x + 1
• 4x³ – 3xy + 2x
• 5ab + 2a + 2

Definição de Polinômios

Chamamos de polinômio uma função P : C → C na variável x que possui a seguinte forma:

• P(x) = a_nxⁿ + a_{n – 1}x^{n – 1} + … + a₁x + a₀

Tal que:

1. a_n, a_{n – 1}, … , a₁ e a₀ são os coeficientes do polinômio;
2. Os expoentes são formados por números naturais.

Monômio, Binômio e Trinômio

Um polinômio é formado pela multiplicação dos elementos de seus termos. Esses termos podem ser chamados de monômio, binômio ou trinômio.

Monômio: um monômio é um termo do polinômio.

Exemplo:

• 3x²
• 2xy
• 5ab

Binômio: um binômio é um polinômio com apenas dois monômios separados por uma operação da aritmética (adição ou subtração).

Exemplo:

• 3x² + 2x
• a²b – ab
• 2x²y – 2xy

Trinômio: um trinômio é um polinômio com três monômios e separados por duas operação da aritmética. (adição ou subtração)

Exemplo:

• ab³ + ab² + 2
• x³ + 2x² – 3

Então, seguindo a lógica, um polinômio é formado por vários monômios.

Grau dos Polinômios

O grau do polinômio é dado pelo valor do maior expoente.

Seja P(x) = a_nxⁿ + a_{n – 1}x^{n – 1} + … + a₁x + a₀ um polinômio. Então, o grau de P(x) é igual a n, se a_n ≠ 0.

Exemplo:

• P(x) = 5x⁶ + 6x⁵ – 2x⁴ – 3x³ + x² + 5x + 3, o grau desse polinômio é 6;
• P(x) = 2x³ + x² + x + 1, o grau desse polinômio é 3;
• P(x) = 2, o grau desse polinômio é 0 (zero).

Para os polinômios nulo não é definido o grau. Um polinômio é considerado nulo quando todos os seus coeficientes forem iguais a zero.

Exemplo:

• P(x) = a_nxⁿ + a_{n – 1}x^{n – 1} + … + a₁x + a₀ é um polinômio nulo, se a_n = a_{n – 1} = … = a₁ = a₀ = 0.

Raiz ou Zero de um Polinômio

A raiz de um polinômio P(x) é um número n tal que P(n) = 0

A raiz ou zero do polinômio é um número qualquer que torna os dois lados do polinômio iguais.

Exemplo:

• Raiz: 1
  • 2x² – 2x = 0
  • 2(1)² – 2(1) = 0
  • 2 – 2 = 0
  • 0 = 0
• Raiz: 0
  • 2x² – 2x = 0
  • 2(0)² – 2(0) = 0
  • 0 – 0 = 0

Assim, às duas raízes para esse polinômio são 0 e 1.

Operações com Polinômios

Veja como realizar as 4 operações básicas da aritmética com polinômios.

Adição

A adição de dois ou mais polinômios é feita somando os coeficientes dos termos em que o grau coincide.

Exemplo:

1. A(x) = 2x³ + 2x² – 3x + 1
2. B(x) = x³ + 3x² – 2x + 2

A(x) + B(x) = (2x³ + 2x² – 3x + 1) + (x³ + 3x² – 2x + 2) = (2 + 1)x³ + (2 + 3)x² + (- 3 – 2)x + (1 + 2) = 3x³ + 5x² – 5x + 3

Simples, não é?

Subtração

A subtração de dois ou mais polinômios acontece da mesma forma, subtraem-se os coeficientes dos termos coincidentes.

Exemplo:

1. A(x) = 3x³ + 2x² – 2x + 3
2. B(x) = 2x³ – x² + 5x – 4

A(x) – B(x) = (3x³ + 2x² – 2x + 3) – (2x³ – x² + 5x – 4) = 3x³ – 2x³ + 2x² + x² – 2x – 5x + 3 + 4 = x³ + 3x² – 7x + 7

Super simples também.

Multiplicação

A multiplicação é feita utilizando a propriedade distributiva da multiplicação. Assim, é multiplicado os coeficientes dos termos e conserva-se a variável, caso exista, e os expoentes são somados.

Exemplo 1:

• A(x) = 2x³ + 2x + 1
• B(x) = x² + 2x – 2

A(x) . B(x) = (2x³ + 2x + 1) . (x² + 2x – 2) = (2 . 1)x^{(3 + 2)} + (2 . 2)x^{(3 + 1)} + [2 . (-2)]x³ + (2 . 1)x^{(1 + 2)} + (2 . 2)x^{(1 + 1)} + [2 . (-2)]x + (1 . 1)x² + (1 . 2)x + [1 . (-2)] = 2x⁵ + 4x⁴ – 4x³ + 2x³ + 4x² – 4x + x² + 2x – 2 = 2x⁵ + 4x⁴ – 2x³ + 5x² – 2x – 2

Exemplo 2:

• A(x) = 2x³ – 3x + 2
• B(x) = 4x³ + x² – 1

A(x) . B(x) = (2x³ – 3x + 2).(4x³ + x² – 1) = 8x⁶ + 2x⁵ – 2x³ – 12x⁴ – 3x³ + 3x + 8x³ + 2x² – 2 = 8x⁶ + 2x⁵ – 12x⁴ + 3x³ + 2x² + 3x – 2

Divisão

Na divisão de polinômios vamos utilizar um método conhecido como método da chave. Que consiste na divisão de dois polinômios A(x) e B(x), não nulos. Nessa divisão obteremos os polinômios Q(x), o quociente, e R(x), o resto.

Logo,

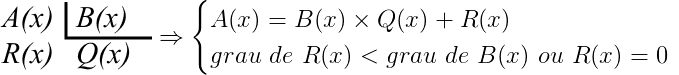
Onde:

• A(x): é o dividendo;
• B(x): é o divisor;
• Q(x): é o quociente;
• R(x): é o resto.

Para ficar mais claro vamos aplicar o método em um exemplo prático.

Exemplo:

Seja os polinômios A(x) = 3x³ + 2x² + 2x – 1 e B(x) = x² + x + 2

Agora vamos executar o passo-a-passo do método da chave:

Passo 1: primeiro é necessário verificar se o grau do dividendo é maior ou igual ao grau do divisor. Se não for, não será possível fazer a divisão. Nos polinômios do exemplo, o grau de A(x) = 3 e B(x) = 2. Tudo certo.

Passo 2: devemos escrever os polinômios da seguinte forma:

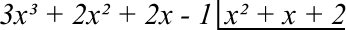
Passo 3: Agora, dividimos o primeiro termos do dividendo pelo primeiro termo do divisor:

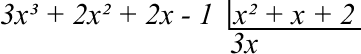
Passo 4: nesse passo, devemos multiplicar 3x por todos os termos do divisor, começando da direita para a esquerda. O resultado do produto deve ser colocado embaixo de cada termo coincidente no dividendo e com o sinal trocado. Finalmente, devemos somar os termos no dividendo:

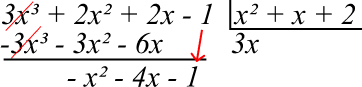
Passo 4: agora, devemos dividir o resultado da soma anterior pelo divisor. Pegamos o primeiro termo do resultado da soma anterior (-x²) e dividimos pelo maior termo do divisor (x²):

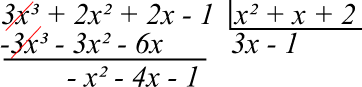
Passo 5: repita o processo até que o grau do resto R(x) seja menor que o grau do divisor B(x) ou o grau do resto R(x) ser 0 (zero).

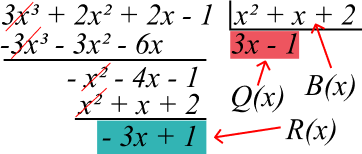
Portanto, como o grau de R(x) é menor que o grau de B(x), temos que parar por aqui. O resultado da divisão de A(x) = 3x³ + 2x² + 2x – 1 e B(x) = x² + x + 2 é: Q(x) = 3x – 1

Exercícios

Veja os exercícios sobre operações com polinômios nos links a seguir:

• Operações com polinômios
• Divisão de polinômios