A distância entre dois pontos na geometria é uma medida entre um ponto A e um ponto B estabelecida por um segmento de reta entre esses pontos. A medida entre os pontos equivale à medida do segmento de reta que ligam eles.
Distância entre pontos no plano cartesiano
No plano cartesiano conseguimos encontrar a distância através do par ordenado (x, y). Isso só é possível quando os pontos A e B estão alinhados horizontalmente ou verticalmente.
Quando os pontos estiverem em outra posição, como na diagonal, por exemplo, precisamos calcular a distância de outra forma.
Exemplo:
1) Encontre a distância entre A(2, 2) e B(3, 2):

A distância entre A e B é:
d(A, B) = B(3, 2) – A(2, 2) = 3 – 2 = 1
1) Qual a distância entre A(1, 3) e B(3, 1)?

Perceba que a distância entre os pontos dados forma um triângulo retângulo com catetos mediando 2 e 2, a outra medida equivale à medida da hipotenusa.
Para encontrar a medida entre os pontos, neste caso, podemos usar o Teorema de Pitágoras. Veja:
[d(A, B)]² = 2² + 2² = √8 = 2√2
Fórmula para calcular a distância entre pontos
Para calcular a distância entre dois pontos temos a fórmula a seguir:
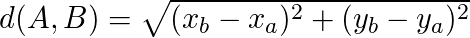
Essa fórmula serve para calcular a distância no plano cartesiano em que temos as coordenadas associadas a cada ponto. Por exemplo, A(x1, y1) e B(x2, y2).
Exemplo:
1) Calcule a distância entre A(2, 3) e B(3, 1).
Aplicando a fórmula, temos:
d(A, B) = √((2 – 3)² + (3 – 1)²) = √((-1)² + 1²) = √(1 + 1) = √2
Leia mais sobre o assunto:
Distância entre dois pontos no espaço
Para calcular a distância no espaço, devemos considerar agora três coordenadas associadas, as coordenadas x, y e z.
Da mesma forma que no plano de duas coordenadas, quando os pontos estão horizontalmente ou verticalmente é fácil ver visualmente a medida equivalente à distância entre eles.
Porém, quando eles estão diagonalmente no espaço, por exemplo, precisamos de outra forma para calcular a distância entre eles.
Exemplo:
1) Calcule a distância entre A(2, 1, 0) e B(3, 2, 0).
Veja que nos pontos a coordenada z possui valor igual a 0, dessa forma os pontos estão no plano e não no espaço.

Então, a distância entre eles é:
[d(A, B)]² = (3 – 2)² + (2 – 1)² = 1² + 1² = √2
Fórmula da distância no espaço
Generalizando, podemos calcular a distância entre A e B no espaço usando a seguinte fórmula:
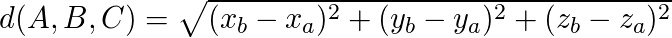
Exemplo:
1) Calcule a distância entre A(1, 2, 3) e B(4, 3, 1).
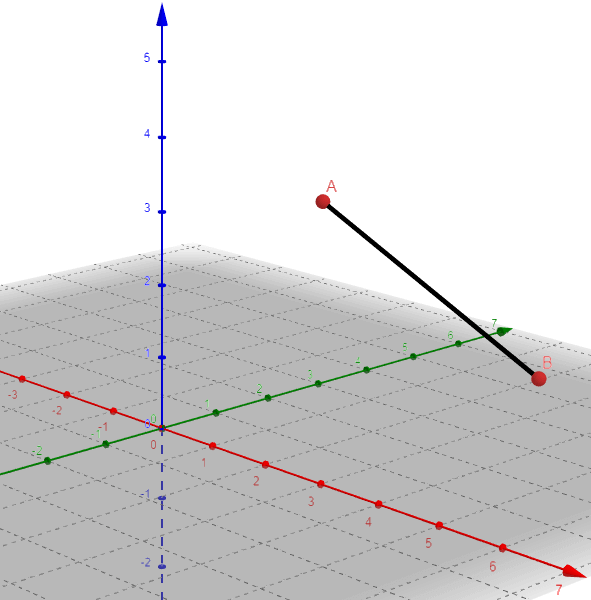
d(A, B, C) = √((4 – 1)² + (3 – 2)² + (1 – 3)²) = √(3² + 1² + (-2)²) = √(9 + 1 + 4) = √14
Leia mais sobre o assunto:
Créditos: Imagens geradas no Geogebra.
Exercícios
Acesse os exercícios no link a seguir:



