O paralelepípedo é um sólido geométrico com faces paralelas. O paralelepípedo é uma figura tridimensional e é uma das figuras geométricas estudas pela geometria espacial.

Definição
Podemos definir o paralelepípedo como uma figura tridimensional em que suas faces são paralelogramos. Dessa forma, existem três maneiras de defini-lo:
- É um prisma em que sua base é um paralelogramo;
- É um hexaedro em que cada face seja um paralelogramo;
- É um hexaedro com três pares de faces paralelas.
Elementos
Um paralelepípedo é formado pelos seguintes elementos:
- Faces: Possui 6 faces. As faces são os lados formados pela união das arestas.
- Vértices: Possui 8 vértices. Os vértices são pontos onde as arestas se encontram;
- Arestas: Possui 12 arestas. As arestas são segmentos de retas ligadas nos vértices que formam as faces.
Tipos de Paralelepípedo
Podemos classificar os paralelepípedos conforme sua disposição no espaço:
Retos: é quando as faces laterais são perpendiculares, ou seja, as arestas formam ângulos retos (90°) com as bases. Dessa forma, é chamado também de paralelepípedo retângulo.

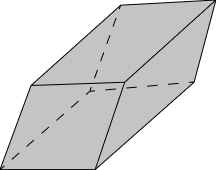
Oblíquos: é oblíquo quando não são retos, ou seja, quando as faces laterais não formam ângulos retos e assim elas não são perpendiculares.
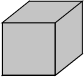
Isósceles: é quando todas as faces são quadradas, quando isso acontece chamamos o paralelepípedo de cubo.
Planificação
Se “abrirmos” o paralelepípedo veremos que suas faces são formadas por outas figuras geométricas. Isso é o que se chama de planificação. É importante para entendermos como calcular a área desse hexaedro.

Pela figura percebemos que as bases e as faces são formadas por retângulos, mas dependendo do tipo podem ser formadas por quadrados também.
Como Calcular a Área?
Para calcular a área do paralelepípedo devemos entender que ele é uma figura geométrica espacial. Assim, a área será de uma figura tridimensional.
Área da Base
A base é formada por uma figura geométrica plana. Então, para calcular devemos multiplicar a base pela altura dessa figura. Temos a seguinte fórmula:
Ab = b . h
Onde:
- Ab: é a área;
- b: é a medida da base;
- h: é a medida da altura.
Área Lateral
Para calcular a área lateral, temos que entender que o sólido possui quatro faces laterais formando pares. Então, para calcular a área lateral, usamos a seguinte fórmula:
- Al = ac + bc + ac + bc ⇒
- Al = 2ac + 2bc ⇒
- Al = 2(ac + bc)
Onde:
- Al: é a área;
- a, b e c: são as medidas das arestas.
Área Total
Para calcular a área total, temos que olhar para a figura planificada do paralelepípedo. Assim, a área total é a soma dos pares das faces opostas. Temos a seguinte fórmula:
At = 2(ab + ac + bc)
Onde:
- At: é a área;
- a, b e c: são as medidas das arestas.
Volume do Paralelepípedo
Para calcular o volume devemos proceder da mesma forma que calculamos o volume do cubo. O volume do cubo é o produto do comprimento, da largura e altura. Então, temos a seguinte fórmula para o volume do paralelepípedo:
V = a . b . c
Onde:
- V: é o volume;
- a, b e c: são as medidas das arestas.
Que é equivalente dizer que o volume é a medida da área da base pela altura.
Exercícios
Acesse os exercícios no link a seguir:



