Veja os exercícios abaixo que preparamos para você fixar o conteúdo aprendizado sobre o paralelepípedo.
1) Considere uma caixa de água com formato de um paralelepípedo reto retângulo totalmente cheia, com comprimento de 7 m e largura de 4 m e altura de 2 m. Calcule:
a) A área da base
b) A área lateral
c) A área total
d) O volume de água da caixa
Ver resposta
a) A área da base desta caixa é calculada pela fórmula do retângulo, pois a base da caixa é retangular: Ab = comprimento x largura
Ab = 7 x 4 = 28 m²
b) A área da lateral de um paralelepípedo é calculada pela fórmula: Al = 2((comprimento x altura) + (largura x altura)) = 2((7 x 2) + (4 x 2)) = 2(14 + 8) = 2 . 22 = 44 m²
c) A área total do paralelepípedo é: At = 2((comprimento x largura) + (comprimento x altura) + (largura x altura)) = 2((7 x 4) + (7 x 2) + (4 x 2)) = 2(28 + 14 + 8) = 2 . 50 = 100 m²
d) O volume de um paralelepípedo é: V = (comprimento x largura x altura) = 7 x 4 x 2 = 56 m³
2) Uma fábrica produz tijolos no formato de paralelepípedos e de cubos, com volume igual. Sabendo que os tijolos no formato de paralelepípedo têm 5 cm de largura, 10 cm de comprimento e 2 cm de altura. A medida dos lados dos tijolos que têm o formato de cubo é igual a:
a) 4,64 cm
b) 7,1 cm
c) 10 cm
d) 20,4 cm
e) 35 cm
Ver resposta
O volume do paralelepípedo é:
Volume paralelepípedo = 10 x 5 x 2= 100 cm³
Como a questão diz que o paralelepípedo e o cubo possuem volumes iguais, então:
Volume paralelepípedo = Volume cubo
Considerando a como a medida da aresta do cubo, então:
Volume cubo = a³
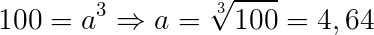
Logo, as arestas dos tijolos com formato de cubo possuem um tamanho aproximado de 4,64 cm.


