A função inversa é uma função que é ao mesmo tempo, injetora e sobrejetora, dessa forma ela é bijetora.
É obtida trocando o domínio pela imagem da função. Assim, a inversa de uma função qualquer modifica o domínio e a imagem, isto é, o domínio vira a imagem e a imagem vira o domínio.
Função Injetora, Sobrejetora e Bijetora
-
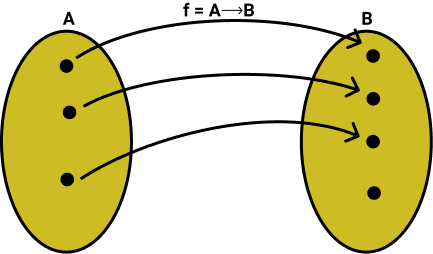
Injetora: uma função é injetora quando todos os elementos distintos do domínio possuem imagens distintas
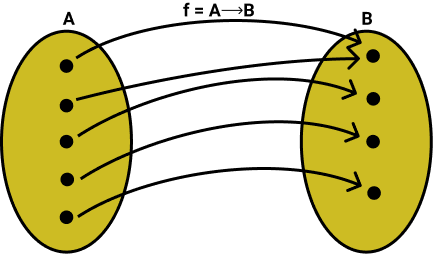
- Sobrejetora: uma função é sobrejetora quando cada elemento da imagem possuem pelo menos um elemento correspondente no domínio.
-
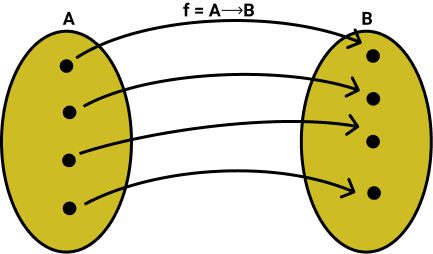
Bijetora: uma função é bijetora quando ela é injetora e sobrejetora.
Notação
Na matemática uma função f = A → B tem a inversa definida por f-1: B → A, ou seja, a inversa é obtida trocando o domínio pela imagem e vice-versa.
Exemplo:
Seja A = {1, 2, 3} e B = {2, 4, 5}, veja como é a inversa:
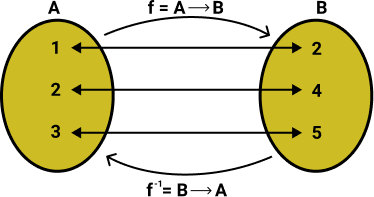
Então, o domínio de f é a imagem de f-1, e a imagem de f é o domínio de f-1.
Obtendo a Função Inversa de uma Função qualquer
Seja f: R → R, função bijetora, e f-1: R → R a inversa da função f.
Então, para determinamos a inversa, devemos proceder da seguinte forma:
- Exemplo 1:
- f(x) = x – 1
- y = x – 1
- x = y + 1
- y = x + 1
- f-1(x) = x + 1
- Exemplo 2:
- f(x) = 2x + 1
- y = 2x + 1
- y – 1 = 2x
- x = (y – 1)/2 (troca x por y e vice-versa)
- y = (x – 1)/2
- f-1(x) = (x – 1)/2
Leia também
Exercícios
Veja os exercícios propostos no link a seguir:

