A função modular é uma função em que em seus elementos são aplicados o módulo na sua lei de formação.
O módulo ou valor absoluto, representado por duas barras verticais |a|, é um número real a, em que nesse número é desconsiderado o seu sinal.
Exemplo:
- |2| = 2
- |-2| = 2
- |3| = 3
- |-3| = 3
Então temos apenas duas possibilidades na função modular:
- |x| é x, se x ≥ 0
-
Exemplo:
- |0| = 0
- |2| = 2
-
Exemplo:
- |-x| é x, se x < 0
-
Exemplo:
- |-2| = 2
- |-5| = 5
-
Exemplo:
O sinal é desconsiderado.
Definição
A função modular é definida da seguinte forma:
Seja f: R → R uma função e f(x) = |x|, assim:
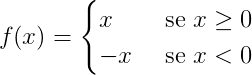
Gráfico
O gráfico desse tipo de função muda a direção do gráfico para positivo quando há a intersecção com o eixo x.
Sabemos que os valores abaixo do eixo x são valores negativos e na função modular os valores negativos são desconsiderados o sinal.
Exemplos:
f(x) = x

f(x) = |x|

f(x) = x² + 2x – 3
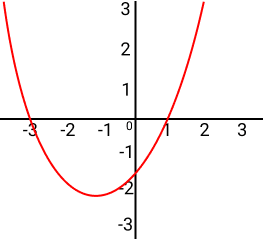
f(x) = |x² + 2x – 3|

Propriedades
- |x| = |-x| com x ∊ R;
- |x²| = |x|² = x² com x ∊ R;
- |x . y| = |x| . |y|, com x e y ∊ R;
- |x + y| ≤ |x| + |y|, com x e y ∊ R.
Exercícios
Link para os exercícios abaixo:



