Aprenda a calcular a inversa de uma função resolvendo estes exercícios.
1) Seja a função f: R -> R, definida por
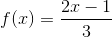
, calcule
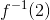
Ver resposta
Termos que começar a responder à questão fazendo a permutação das variáveis, assim:
A função dada é:
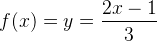
Após permutar as variáveis, temos:
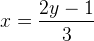
Agora vamos expressar y em função de x:
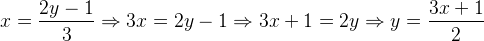
Então, a função inversa de f é:
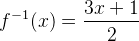
Portanto, 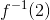é igual a:
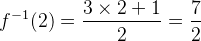
2) Determine a função inversa de f, de R – {5} em R – {-1}, definida por
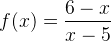
Ver resposta
Temos que a função dada no problema é:
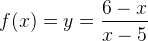com y ≠ -1 e x ≠ 5
Permutando as variáveis, temos:
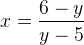com x ≠ -1 e y ≠ 5
Agora expressaremos y em função de x:
Portanto, a inversa de f, de R – {5} em R – {-1} é:
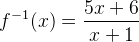
3) Determine a função inversa das seguintes funções:
a) y = 4x + 3
b) y = 7x
c) y = 6x – 2
d) y = 9x -3
e) y = -x + 7
Ver resposta
a)
y = 4x + 3 permutando x com y ⇒
x = 4y + 3 isolando y ⇒
-4y = 3 – x ⇒
y = (3 – x)/-4 ⇒
y = (x – 3)/4
b)
y = 7x ⇒
x = 7y ⇒
y = x/7
c)
y = 6x – 2 ⇒
x = 6y – 2 ⇒
x + 2 = 6y ⇒
y = (x + 2)/6
d)
y = 9x -3 ⇒
x = 9y – 3 ⇒
x + 3 = 9y ⇒
y = (x + 3)/9
e)
y = -x + 7 ⇒
x = -y + 7
y = 7 – x
4) Seja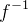 
a função inversa de f: R -> R, definida por f(x) =
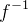7x – 3, então (4)
é igual a:
a) 1
b) 2/3
c) -1/3
d) -4
e) 5/2
Ver resposta
A função dada é: f(x) = y = 7x – 3
Permutando das variáveis, temos:
x = 7y – 3
Expressando y em função de x, temos que:
x = 7y – 3 ⇒
x + 3 = 7y ⇒
y = (x + 3)/7
Portanto, 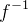(4) = (4 + 3)/7 = 7/7 = 1
