Pirâmide: Definição, Tipos, Área e Volume

A pirâmide é um poliedro com uma base formada por um polígono e as faces formadas por triângulos, unidas em um vértice a uma certa altura.

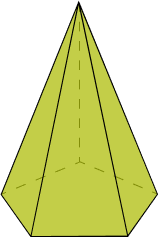
Definição

Seja um plano α, um ponto V, de forma que V ∉ α, uma área poligonal S no plano α, chamamos de pirâmide a união dos segmentos de retas VP onde P ∈ S.

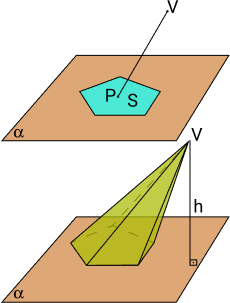
Elementos

As pirâmides possuem os seguintes elementos na sua formação:

• Arestas laterais: as arestas laterais são os segmentos de retas que iniciam no vértice da base poligonal até o vértice comum da pirâmide;
• Faces laterais: as faces laterais são formadas pelas regiões triangulares definidas pelas arestas laterais;
• Arestas da base: a região poligonal que forma a base possuem lados, e esses lados são segmentos de retas ligando os pontos da base e formandos as arestas;
• Altura: a altura é definida pelo segmento de reta perpendicular que liga seu vértice comum até a base;
• Apótema: apótema é a altura da face da pirâmide.

Tipos de Pirâmides

As pirâmides são classificadas conforme o número de lados que compõe sua base:

Triangular: uma pirâmide é triangular quando a base é um triângulo. É também chamada de tetraedro:

Quadrangular: uma pirâmide é quadrangular quando sua base é um paralelogramo ou mais especificamente um quadrado:

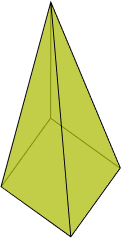
Pentagonal: uma pirâmide é pentagonal quando a sua base é um pentágono, ou seja, o polígono de cinco lados:

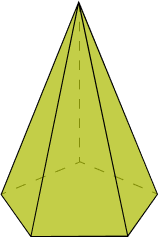
Hexagonal: uma pirâmide é hexagonal quando sua base é um hexágono, ou seja, é formada por um polígono com seis lados:

Octogonal: quando a base é composta por um octógono, isto é, um polígono de oito lados:

Classificação

As pirâmides são classificadas em:

Retas: uma pirâmide é reta quando a altura é perpendicular a base;

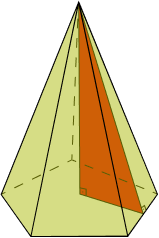
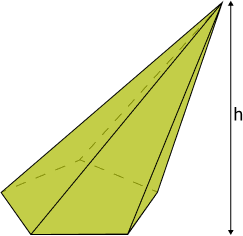
Oblíquas: uma pirâmide é oblíqua quando não é reta:

Regulares: quando a base é composta por um polígono regular:

Não Regulares: quando a base não é composta por um polígono regular.

Área

A área é a soma das áreas da base e da lateral da pirâmide.

Área Lateral

Como a área lateral de uma pirâmide tem um formato triangular, a área lateral é calculada utilizando a fórmula da área do triângulo.

A = (b . h)/2

Onde:

• A: é a área do triângulo;
• b: é a base;
• h: é a altura.

Então, calcula-se a área de uma face triangular e multiplica pela quantidade de faces laterais ou soma uma a uma as áreas laterais das faces que o triângulo possui.

Assim:

A_L = A₁ + A₂ + A₃ +, …, + A_n,

Onde:

• A₁ + A₂ + A₃ +, …, + A_n são as áreas das faces laterais.

Área da Base

A área da base depende do tipo de pirâmide. Se for triangular, a área da base é calculada usando a fórmula da área do triângulo, se for quadrangular a área da base é calculada pela fórmula da área do paralelogramo, e assim por diante.

Área Total

Por fim, a área total é a soma da área da base com a área lateral.

A área total é calculada pela seguinte fórmula:

A_T = A_B + A_L

Onde:

• A_T: é a área total;
• A_B: é a área da base;
• A_L: é a área lateral.

Volume

O volume é calculado pela seguinte fórmula:

V = ¹⁄₃ . A_B . h

Onde:

• V: é o volume;
• A_B: é a área da base;
• h: é a altura.

Exercícios

Acesse os exercícios sobre a pirâmide no link a seguir:

• Exercícios sobre a pirâmide