As funções trigonométricas são funções angulares obtidas através do auxílio do círculo trigonométrico.
Destacamos as principais funções trigonométricas:
- Função Seno;
- Função Cosseno;
- Função Tangente.
Considerando um número real x qualquer e um ponto P do círculo trigonométrico, associamos esse ponto a um único valor para as funções trigonométricas seno e cosseno, e chamaremos sen(x) e cos(x).
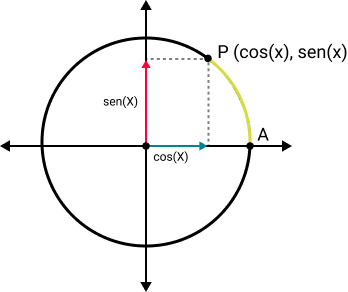
Esse ponto P mostrado acima pode ser qualquer um dos valores do círculo trigonométrico, em graus ou radiano.
Função Trigonométrica Seno
A função seno é uma função periódica que possui imagem no intervalo [-1, 1], isto é, -1 ≤ sen(x) ≤ 1, onde x é um número real.
Domínio
O domínio da função é o conjunto dos números reais, ou seja, sen(x) é definido para qualquer x real, então o domínio de f(x) = sen(x) é o conjunto R. Logo: D = R
Imagem
A função sen(x) assume o valor máximo igual a 1, isso ocorre quando o valor de x representa um arco com primeira determinação π/2. E o valor mínimo igual a -1, quando x representa um arco com primeira determinação 3π/2.
Então, o conjunto imagem para a função f(x) = sen(x) é o intervalo [-1, 1], assim: Im = [-1, 1]
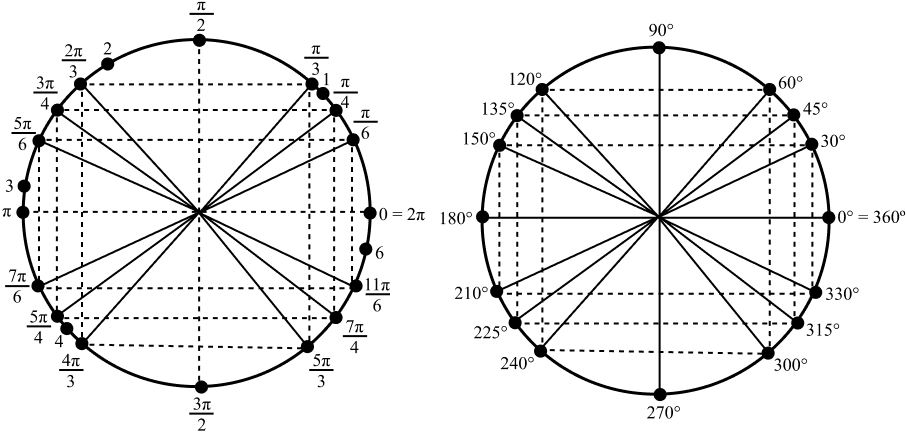
Arcos Notáveis
Os arcos notáveis são valores, em radianos, para os ângulos 0°, 30°, 45°, 60°, 90°, 180°, 270° e 360°.
Então, assumindo que x seja um dos valores notáveis acima, temos a seguinte tabela com os valores em radianos para os ângulos em graus e o seno para o respetivo ângulo.
| x | sen(x) |
|---|---|
| 0 | 0 |
| π/6 | 1⁄2 |
| π/4 | √2/2 |
| π/3 | √3/2 |
| π/2 | 1 |
| π | 0 |
| 3π/2 | -1 |
| 2π | 0 |
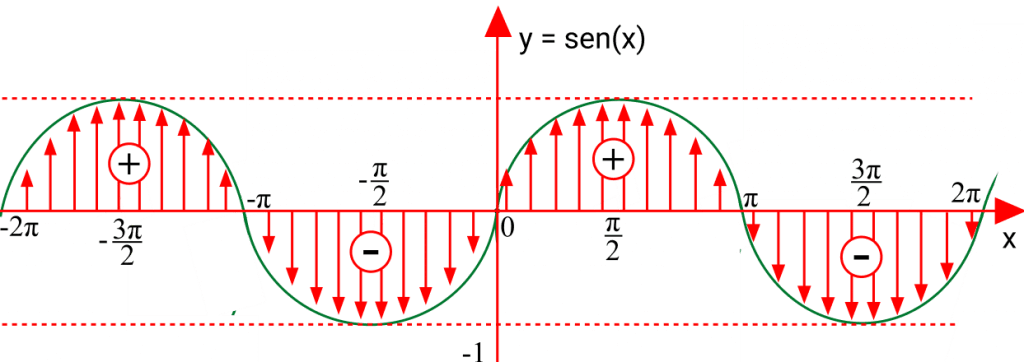
A partir dessa tabela podemos construir o gráfico da função seno.
Gráfico da Função Seno
Vamos construir o gráfico da função colocando os valores notáveis no plano cartesiano. O comportamento da função seno é uma variação entre -1 e 1, por esse motivo o seno é chamada função periódica.
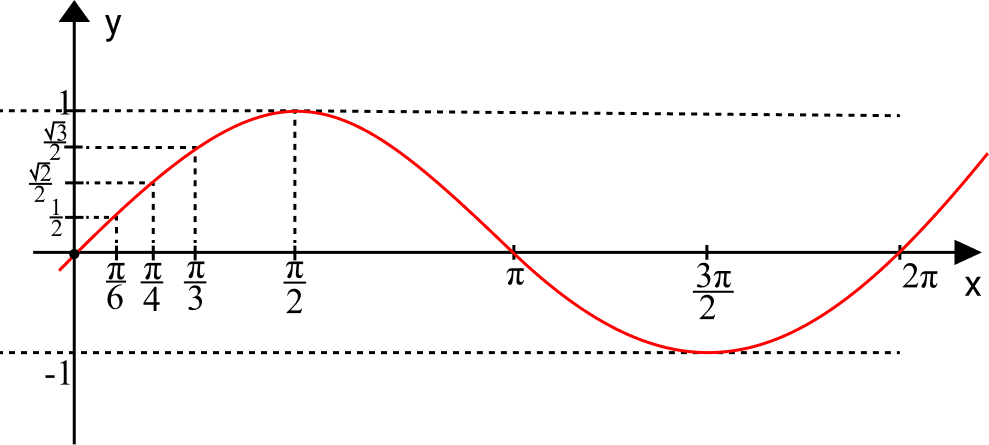
Período
O período é a curva do gráfico no intervalo 0 a 2π, chamado de senoide. Então, o período do seno é 2π.
Paridade
A paridade da função seno é dada por sen(-x) = – sen(x). Assim, f(x) = sen(x) é ímpar.
Sinal
No círculo trigonométrico a função tem sinal positivo nos quadrantes I e II, e sinal negativo nos quadrantes III e IV. Considerando uma volta completa no ciclo.
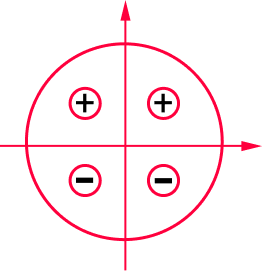
Pelo gráfico podemos ver quando a função assume valores negativos, positivos e zero.
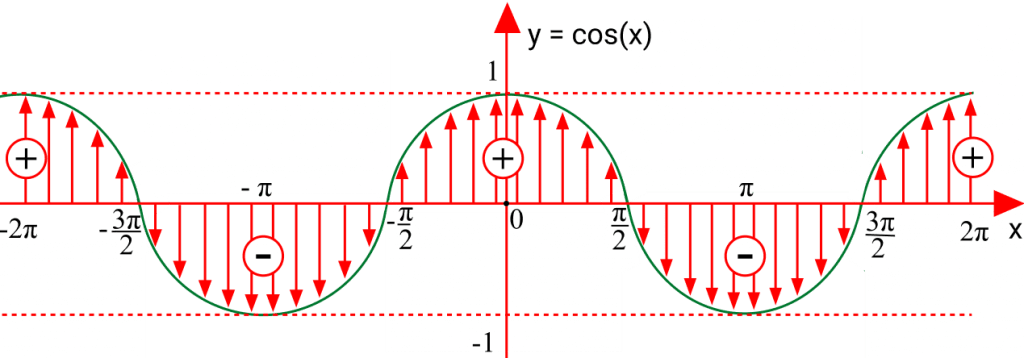
Função Trigonométrica Cosseno
A função cosseno também é uma função periódica que possui imagem no intervalo [-1, 1], isto é, para um x real -1 ≤ cos(x) ≤ 1.
Domínio
O domínio da função cosseno é o conjunto dos números reais, isto é, cos(x) é definido para qualquer x real, então o domínio de f(x) = cos(x) é o conjunto R. Assim: D = R
Imagem
A função cos(x) assume valor máximo igual a 1, ocorre quando o valor de x representa um arco com primeira determinação 0. E o valor mínimo igual a -1, quando x representa um arco com primeira determinação π.
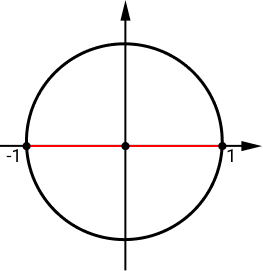
Assim, o conjunto imagem para f(x) = cos(x) é o intervalo [-1, 1]. Logo: Im = [-1, 1]
Arcos Notáveis
Os arcos notáveis são valores, em radianos, para os ângulos 0°, 30°, 45°, 60°, 90°, 180°, 270° e 360°.
| x | cos(x) |
|---|---|
| 0 | 1 |
| π/6 | √3/2 |
| π/4 | √2/2 |
| π/3 | 1⁄2 |
| π/2 | 0 |
| π | -1 |
| 3π/2 | 0 |
| 2π | 1 |
Esses valores nos auxiliará na construção do gráfico da função cosseno.
Gráfico
Usando os valores dos arcos notáveis acima, vamos construir o gráfico da função no plano cartesiano. A função cosseno é uma variação entre -1 e 1. Também é uma função periódica.

Período
O período é a curva do gráfico no intervalo 0 a 2π, chamado de cossenoide. Então, o período da função é 2π.
Paridade
A paridade é dada por cos(-x) = cos(x). Assim, f(x) = cos(x) é par.
Sinal
No círculo trigonométrico a função cosseno tem sinal positivo nos quadrantes I e IV, e negativo nos quadrantes II e III. Considerando uma volta completa no ciclo.
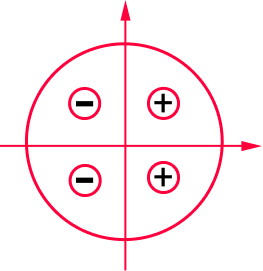
Pelo gráfico podemos ver quando a função cosseno assume valores negativos, positivos e zero.
Função Trigonométrica Tangente
A função tangente para um número real x é a razão entre o seno e o cosseno desse número. É uma função ilimitada, ou seja, não é limitada por um intervalo como as funções seno e cosseno, mas é periódica.
Domínio
A função tangente existe, se, e somente se, o cos(x) ≠ 0, então definimos o domínio da função f(x) = tan(x) como:
D = {x ∈ R | x ≠ π/2 + kπ, k ∈ Z}
Imagem
A tangente de um número real x pode assumir qualquer valor, já que a função tangente é ilimitada. Dessa forma, a imagem da função é:
Im = ]-∞, ∞[
Ou seja, pode assumir infinitos valores negativos ou positivos.
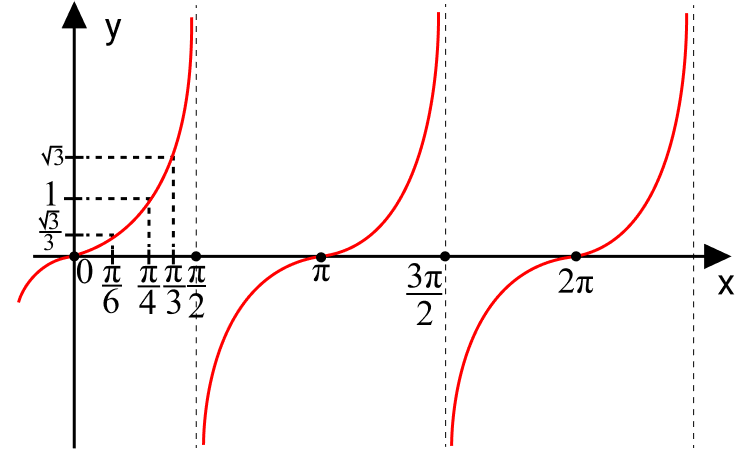
Arcos Notáveis
Os arcos notáveis são valores, em radianos, para os ângulos 0°, 30°, 45°, 60°, 90°, 180°, 270° e 360°.
| x | tan(x) |
|---|---|
| 0 | 0 |
| π/6 | √3/3 |
| π/4 | 1 |
| π/3 | √3 |
| π/2 | ∄ |
| π | 0 |
| 3π/2 | ∄ |
| 2π | 0 |
Este símbolo (∄) significa não existe.
Esses valores nos auxiliará na construção do gráfico da função tangente.
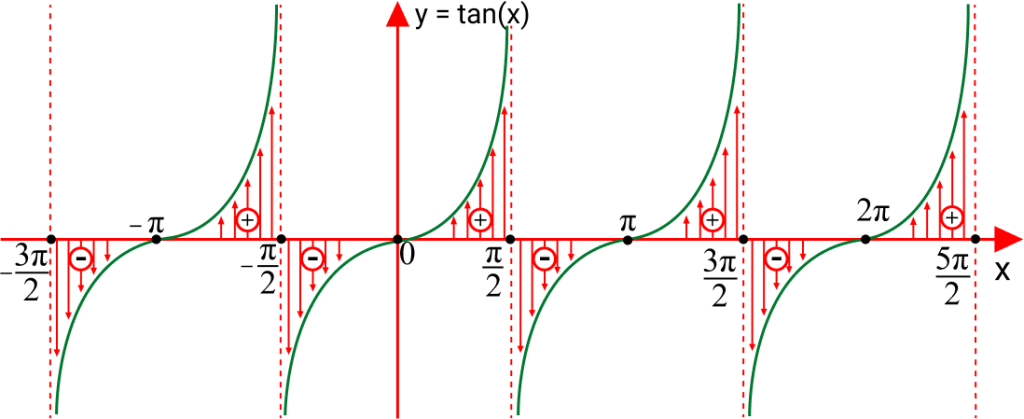
Gráfico
Com os valores notáveis para a função em mãos, vamos construir o gráfico. A função tangente é ilimitada, isto é, não está dentro de um intervalo. É uma função periódica, ou seja, ocorre em determinados períodos.
Período
O período da função é π.
Paridade
A paridade da função é dada por tan(-x) = – tan(x). Assim, f(x) = tan(x) é ímpar.
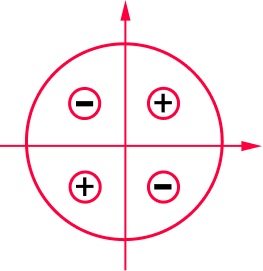
Sinal
No círculo trigonométrico a função tangente tem sinal positivo nos quadrantes I e III, e negativo nos quadrantes II e IV. Considerando uma volta completa no ciclo.
Pelo gráfico podemos ver quando a função assume valores negativos, positivos e zero.
Esse é um resumo das funções trigonométricas mais importantes da trigonometria.
Exercícios de trigonometria
Veja os exercícios no link abaixo:


