Veja alguns exercícios sobre o teorema de Pitágoras para auxiliar no aprendizado sobre estes assuntos bastante importantes para a matemática.
1) Considere um triângulo isósceles com dois lados medindo 10 cm e base de 12 cm. Calcule a altura deste triângulo.
Ver resposta
Em um triângulo isósceles a altura divide a base na metade e por esse motivo temos a formação de dois triângulos retângulos.

Dessa forma, podemos calcular a medida da altura h através do teorema de Pitágoras.
Portanto, temos que:
a² = h² + b² ⇒ 10² = h² + 6² ⇒ 100 = h² + 36 ⇒ h² = 100 – 36 ⇒ h² = 100 – 36 ⇒ h = √64 = 8
Perceba que a base foi dividida ao meio, logo temos que considerar 12/2 = 6.
2) Seja um triângulo equilátero, encontre a fórmula da área deste triângulo.
Ver resposta
Um triângulo equilátero possui todos os lados com as mesmas medidas.
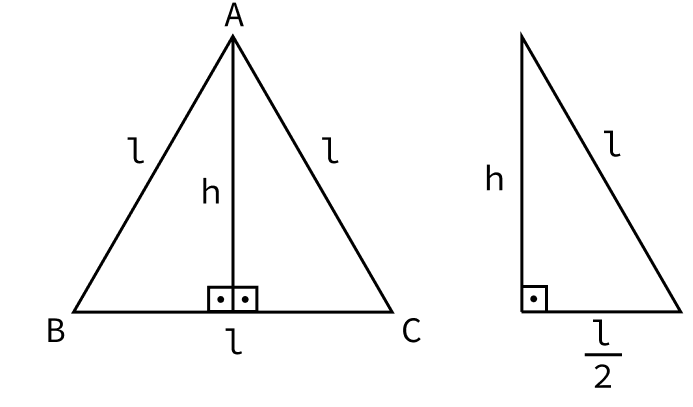
Neste tipo de triângulo, a altura também divido-o em dois triângulos retângulos. Sendo assim, podemos aplicar o teorema de Pitágoras para encontrar a altura.
Então: l² = h² + (l/2)² ⇒ h² = l² – (l/2)² ⇒ h² = l² – l²/4 ⇒ h² = l² – l²/4 ⇒ h² = (4l² – l²)/4 ⇒ h² = 3l²/4 ⇒ h = √3l²/4 ⇒ h = l√3/2
Logo, a altura do triângulo equilátero é calculada pela fórmula h = l√3/4, onde l é a medida do lado do triângulo.
Agora, para encontrarmos a fórmula da área do triângulo equilátero, vamos usar a fórmula geral da área do triângulo: A = (b . h)/2
Portanto, temos que: A = (b . h)/2 ⇒ A = (l . (l√3/2))/2 ⇒ A = (l²√3/2)/2 ⇒ A = l² . √3/2 . 1/2 ⇒ A = l²√3/4
Como a base tem medida l, então trocamos na fórmula b por l.
3) Calcule a medida da hipotenusa de um triângulo retângulo com cateto adjacente medindo 5 cm e cateto oposto medindo 4 cm.
Ver resposta
A hipotenusa é calculada por:
a² = b² + c² ⇒ a² = 5² + 4² ⇒ a² = 25 + 16 ⇒ a² = 41 ⇒ a = √41 ⇒ a = 6,4
Portanto, a medida relacionada a hipotenusa é de aproximadamente 6,4 cm.
4) Determine a fórmula que serve para encontrar a medida relacionada a diagonal de um quadrado.
Ver resposta
Sabemos que um quadrado possui todos os lados com a mesma medida, e se traçarmos a diagonal de um quadrado, o dividimos em dois triângulos retângulos.

Dessa forma, podemos aplicar o teorema de Pitágoras para encontrar a medida da diagonal.
Então: d² = L² + L² ⇒ d² = 2L² ⇒ d² = 2L² ⇒ d = √2L² ⇒ d = L√2
Portanto, a fórmula que calcula a medida da diagonal do quadrado é: d = L√2
Onde L é a medida dos lados do quadrado.
5) Encontre a fórmula que calcula a medida da diagonal do retângulo.
Ver resposta
O retângulo possui seus respectivos lados paralelos iguais, e seus ângulos internos medem 90°. Assim, se traçarmos a diagonal temos a formação de dois triângulos retângulos.

Então, aplicando Pitágoras, temos:
d² = L1² + L2² ⇒ d² = L1² + L2² ⇒ d = √(L1 + L2)
Portanto, a fórmula que calcula a diagonal do retângulo é: d = √(L1 + L2)
Onde L1 e L2 são as medidas dos lados do retângulo.
Exercícios sobre aplicações do teorema de Pitágoras para entender a sua importância para a matemática.
Veja também…

