Estatística é a área da matemática que coleta, analisa e interpreta dados experimentais utilizando teorias probabilísticas para explicar a ocorrência de eventos.
População e Amostra
Na estatística, população é o conjunto total dos dados e amostra é um subconjunto da população.
População
População é o conjunto de elementos que possuem características em comum. É um termo bem mais amplo que no senso comum, podendo haver reunião de pessoas, objetos ou até mesmo ideias.
Exemplo:
Todas as pessoas com ensino superior no Brasil.
Amostras
Amostras, na estatística, são subconjuntos da população e possuem as mesmas características que a população tem. A técnica de retirada de uma amostra da população é chamada amostragem.
Exemplo:
2000 pessoas com ensino superior no Brasil.
Parâmetros
Os parâmetros são as características numéricas da população.
Exemplo:
As médias das notas das pessoas com ensino superior no Brasil.
Estimativas
Torna-se caro e demorado trabalhar com a população inteira, por isso que são escolhidas amostras que possuem as mesmas características da população.
A estimativa é uma medida numérica que descreve uma característica da amostra, que será avaliada e obtido um parâmetro que descreve uma característica da população.
Distribuição de Frequências
Quando se faz um levantamento sobre uma população, é retirada uma amostra dessa população, obtendo dados relativos à amostra e organizando esses dados em tabelas e gráficos, separando-os por classes ou categorias, contendo um número de elementos correspondentes para cada uma das variáveis.
Medidas de Dispersão
As medidas de dispersão servem para indicar o quanto os dados estão dispersos em torno da região central.
Amplitude
A amplitude (H) ou intervalo total é calculada pegando os valores extremos do conjunto de dados. Pode ser calculada pela seguinte fórmula:
- H = x1 – xn
Onde:
- H: é a amplitude;
- x1: é o primeiro valor;
- xn: é o último valor.
Desvio
O desvio serve para medir a dispersão entre uma variável em relação à medida de tendência central. É calculado pela seguinte fórmula:
- Di = xi – MA
Onde:
- Di: é o desvio;
- xi: é uma variável qualquer;
- MA: é a média aritmética dos dados.
Desvio Médio
O desvio médio é calculado fazendo a diferença entre uma variável pela média. O desvio médio serve para indicar a distância de cada elemento da amostra e o seu valor médio. Para calcular o desvio médio, utilizamos a seguinte fórmula:
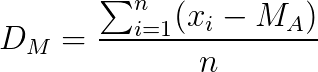
- DM: é o desvio médio;
- xi: é um valor qualquer no conjunto de dados não posição i;
- MA: é a média aritmética;
- n: é o total dos dados do conjunto.
Desvio Padrão
O desvio padrão serve para calcular a uniformidade do conjunto de dados. Assim, quanto mais próximo de 0 (zero), mais próximo da média estão os dados do conjunto.
É calculado utilizando a seguinte fórmula:

Onde:
- DP: é o desvio padrão;
- xi: é um valor qualquer no conjunto de dados não posição i;
- MA: é a média aritmética;
- n: é a quantidade total dos dados do conjunto.
Variância
A variância serve para indicar o quanto disperso estão os dados da média. É calculada utilizando a seguinte fórmula:

Onde:
- V: é a variância;
- xi: é um valor qualquer no conjunto de dados não posição i;
- MA: é a média aritmética;
- n: é o total dos dados do conjunto.
Leia também:
- Desvio Padrão e Variância
- Média Aritmética
- Média Geométrica
- Média Ponderada
- Média, Moda e Mediana
- Probabilidade
- Probabilidade Condicional
Exercícios
Acesse os exercícios no link abaixo:


