A divisão de frações é uma operação de simplificação de duas ou mais frações obtendo um resultado que representa as partes de um número inteiro.
A divisão de fração parece complicado, mas não é tanto assim. Se você já aprendeu como multiplicar frações, basta saber a regra básica e não terá problemas em resolver.
Como fazer divisão de frações?
Para dividir frações o aluno deve manter a primeira fração e multiplicá-la pelo inverso da outra. Veja a seguir alguns exemplos que vão ajudar a entender esse processo. Confira!
Divisão de uma fração por um número natural
Todo número natural pode ser representado por uma fração. Por exemplo, 3 pode ser representado por 3⁄1, já que todo número natural é divisível por 1 (um).
Como o resultado dessa divisão é o próprio número, nós omitimos esse número 1 (um) no denominador.
Dessa forma, quando for dividir um número natural por uma fração ou uma fração por um número natural, tenha em mente a existência desse número “invisível” no denominador.
Assim, para dividir uma fração por um número natural ou um número natural por uma fração, ou até mesmo uma fração por outra fração, basta saber a seguinte regra:
Copia a primeira e multiplica pelo inverso da segunda
Se você não sabe como multiplicar frações, veja o artigo sobre multiplicação de fração antes de seguir.
Exemplos:
Dividir 3 por 4⁄3
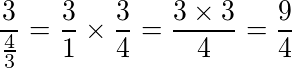
Copiamos a primeira fração, já que
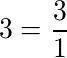
Como todo número natural é uma fração, e invertemos a segunda fração, multiplicando-as.
Dividir 5⁄4 por 5
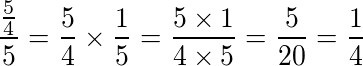
Veja que nesse exemplo ao fazer a inversão do número 5 (cinco) tivemos que considerar o numerador 1 (um). Ou seja, copiamos a primeira, invertemos a segunda, o número de baixo vai para cima e o de cima para baixo, e multiplicamos.
Ao final fizemos a simplificação da fração.
Divisão de uma fração por outra fração
Dividir fração por fração pode parecer um pouco complicado, pois a forma escrita fica um pouco esquisita. Mas é bem simples. Veja!
Dividir 3⁄5 por 7⁄3
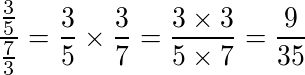
Copiamos a primeira e multiplicamos pelo inverso da segunda. Multiplicando os números de cima e de baixo. Simplificando, se possível, para encontrar uma fração irredutível.
Divisão de várias frações
Essa regra funciona independentemente do número de frações que estamos dividindo. Dividir várias frações em simultâneo, não muda nada, o processo é o mesmo. Veja:
Dividir 3⁄4 por 5⁄7 e por 4⁄5.
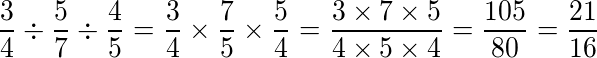
Basta copiarmos a primeira, ou seja, manter como está; invertermos as outras, trocando os numeradores pelos denominadores; por fim, basta fazermos a multiplicação dos numeradores e denominadores das frações.
Simples assim.
Exercícios sobre divisão de frações
Responda os exercícios para fixar o aprendizado.
Veja mais…


