O binômio de Newton é formado por dois monômios elevados a um expoente n. Um valor de n muito grande torna um binômio difícil de calcular e muito grande quando desenvolvido.
Números binomiais são ótimos para utilizar no processo de fatoração de polinômios.
Exemplo:
Considere o binômio (x + y)2, escreva-o na forma expandida.
O expoente indica quantas vezes devemos multiplica a soma (x + y), assim:
- (x + y).(x + y) = x² + xy + xy + y² = x² + 2xy + y²
Número Binomial
Um número binomial é a combinação de um número de n termos k a k. Escrevemos um número binomial da seguinte forma:
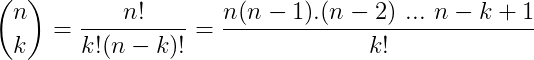
Onde:
- n: é chamado de numerador;
- k: é chamado de denominador;
- n e k são números naturais com n ≥ k.
A expressão do número binomial corresponde a uma combinação simples Cn,k.
Exemplo:
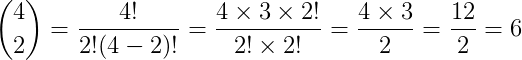
Leia também sobre números fatoriais.
Fórmula do Binômio de Newton
O binômio de Newton é uma potência na forma (x + y)n, com n ∈ R e possui a seguinte fórmula:
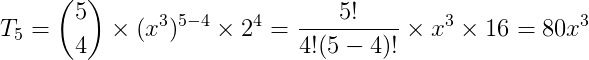
Onde os números binomiais são combinações simples. Dessa forma, quanto maior for o valor de n, mais complexo se torna o binômio.
Exemplo:
Desenvolva o binômio (x + 3)3:
Podemos desenvolver de duas formas: multiplicando os termos ou utilizando a fórmula acima.
- Multiplicando os termos: (x + 3).(x + 3).(x + 3) = (x² + 3x + 3x + 9).(x + 3) = x³ + 3x² + 3x² + 9x + 3x² + 9x + 9x + 27 = x³ + 9x² + 27x + 27;
- Fórmula do binômio: 1 . x³ . 30 + 3 . x² . 3¹ + 3 . x¹ . 3² + 1 . x0 . 33 = x³ + 9x² + 27x + 27.
Para um expoente com valor baixo é simples de fazer, no entanto, para valores altos, calcular um binômio pode ser muito difícil.
Números Binomiais Complementares
Chamamos dois números binomiais de complementares quando eles possuem o mesmo numerador, de forma que a soma dos denominadores seja igual ao numerador.
Exemplo:
Considere os números binomiais abaixo:
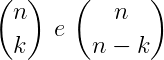
São números binomiais complementares, pois k + n – k = n.
Os números binomiais
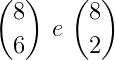
são complementares, pois 6 + 2 = 8.
Propriedade
Se dois números binomiais são iguais, então:
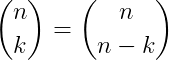
Binômio de Newton e Triângulo de Pascal
O triângulo de Pascal é formado por números binomiais organizados na forma de uma matriz. Onde o numerador de número binomial (n) ocupe a linha e o denominador (k) ocupe a coluna.
Os números binomiais têm a seguinte forma:
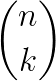
Onde:
- n: são as linhas no triângulo de Pascal;
- k: são as colunas.
Então, o triângulo é formado da seguinte forma:
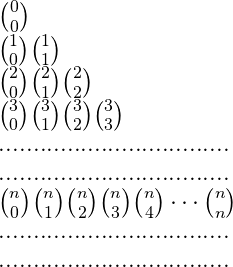
Ao substituirmos os números binomiais pelos valores correspondentes, temos:

Que é o triângulo de Pascal.
Termo Geral do Binômio de Newton
Se quisermos saber um termo qualquer de um binômio devemos utilizar a seguinte fórmula:
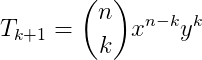
Exemplo:
Encontre o quinto termo de (x³ + 2)5, em que os expoentes de x são decrescentes.
Resolução:
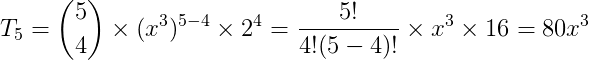
Exercícios
Acesse os exercícios no link a seguir:


