Análise combinatória é a área da matemática que estuda os problemas envolvendo a contagem na ocorrência de um determinado evento, sem a necessidade de reproduzirmos todas as possibilidades.
Fatorial
É importante falarmos sobre fatorial, pois na análise combinatória é comum o uso de fatorial nas fórmulas.
Seja n um número natural, maior que 1, definimos fatorial de n como o produto de todos os números naturais de n até 1.
Simbolicamente, o fatorial de n é: n!
Então, n! = n(n – 1).(n – 2) . … . 3 . 2 . 1
Exemplo:
- 3! = 3 . 2 . 1 = 6
- 10! = 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 3.628.800
Principio Fundamental da Contagem
O princípio fundamental da contagem nos permite definir uma regra de forma que possamos determinar o número de possibilidades de ocorrência de um evento, para que não precisamos reproduzir todas as possibilidades de ocorrência do evento.
Exemplo:
Maria foi a uma loja comprar um par de sapatos. A loja possui três pares de sapatos que interessavam à Maria, em 2 cores diferentes, preto e branco. Quantas possibilidades de escolha Maria tinha para comprar 1 par de sapatos?
Podemos utilizar um diagrama chamado diagrama de árvore para descrever todas as possibilidades que Maria disponha para comprar 1 par de sapatos.

No entanto, descrever todas as possibilidades que Maria possui pode ser um pouco mais complexo. Por exemplo, se ampliássemos as possibilidades para duas ou mais lojas, ou simplesmente a loja disponibilizasse mais opções de cores e modelos à Maria.
Podemos então utilizar do princípio fundamental da contagem para simplificar o problema.
Para cada par de sapato, Maria possui duas possibilidades de escolhas: preto ou branco. Então, vamos chamar de p o número de pares sapatos e c o número de cores disponível.
Onde:
- p = 3;
- c = 2.
Assim, fazendo o produto temos o total de possibilidades que Maria possui para comprar 1 par de sapatos.
p . c = 3 . 2 = 6 possibilidades
Permutação simples
Definimos permutação simples como o número de possibilidades que podemos organizar n elementos distintos em n posições, de forma que cada possibilidade seja diferente da ordem em que os elementos aparecem.
A permutação simples pode ser calculada pela seguinte fórmula:
- Pn = n!
Exemplo:
Em uma eleição para prefeito existem 3 candidatos. Quais as possibilidades dos três candidatos no resultado da eleição?
Solução:
Cada candidato na eleição pode ocupar três posições no resultado da eleição: eleito (primeiro lugar), segundo lugar e terceiro lugar.
Assim, trata-se de um problema de permutação simples.
Logo:
- P3 = 3! = 3 . 2 . 1 = 6
6 possibilidades que podem ocorrer no resultado da eleição.
Permutação com repetição
Na permutação com repetição, na análise combinatória, os elementos do evento são repetidos, diferentemente da permutação simples. Podemos calcular este tipo de permutação utilizando a seguinte fórmula:
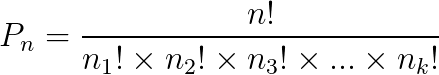
Onde:
- Pn: é a permutação;
- n: total de elementos do evento;
- n1! . n2! . n3! . … . nk!: elementos repetidos no evento.
Exemplo:
Quantos anagramas possuem a palavra CARRO?
Podemos ver que duas letras se repetem. Então, tempos os seguintes dados no problema:
- n: 5 letras;
- n1: 2 letras que se repetem.
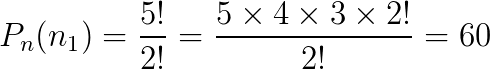
Então, a palavra carro possui 60 anagramas.
Arranjo simples
Arranjo simples é uma forma de agrupar elementos de um conjunto de forma que a maneira a tomar os elementos seja diferente pela ordem e natureza dos elementos.
Podemos calcular um arranjo simples utilizando a seguinte fórmula:
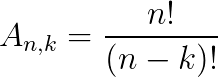
Onde:
- An, k: é o arranjo;
- n: total de elementos do evento;
- k: total de agrupamentos, com k ≤ n;
Exemplo:
Quantos números de 3 algarismos podemos formar com o conjunto abaixo:
- A = {1, 2, 3, 5, 7 e 9}
Temos os seguintes dados:
- n: números de elementos;
- k: quantidades de algarismos por número.
Então:
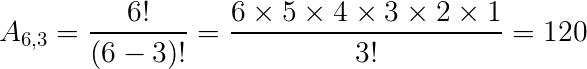
Portanto, podemos formar até 120 número de três algarismos.
Arranjo com repetição
Arranjo com repetição é utilizado quando a ordem dos elementos do evento é importante, sendo que cada elementos pode ser contado mais de uma vez.
Podemos calcular arranjo com repetição utilizando a seguinte fórmula:
- An,k = nk
Onde:
- An,k: é o arranjo com repetição;
- n: total de elementos do evento;
- k: número de elementos escolhidos no evento.
Exemplo:
Seja o conjunto das vogais: A = {a, e, i, o, u}
Se tomarmos o agrupamento de dois em dois, sendo um arranjo com repetição, quantos agrupamentos poderíamos fazer com as vogais do conjunto A?
Temos os seguintes dados:
- A = {a, e, i, o, u};
- n = 5;
- k = 2.
Logo,
- A5,2 = 52 = 25
Então poderíamos fazer 25 combinações diferentes.
Combinação simples
Utilizamos combinação simples quando a ordem dos elementos no evento não importa, porém, cada elemento pode ser contado somente uma vez.
Calculamos uma combinação simples utilizando a seguinte fórmula:
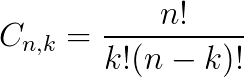
Onde:
- Cn,k: é a combinação simples;
- n: total de elementos dos eventos;
- k: total de agrupamentos do evento, com k ≤ n.
Exemplo:
De quantas maneiras diferentes podemos separar 12 bolas de gudes de cores diferentes, colocando 3 bolas de gudes por pote?
Temos os seguintes dados:
- n = 12 bolas de gudes;
- k = 3 bolas de gudes por pote.
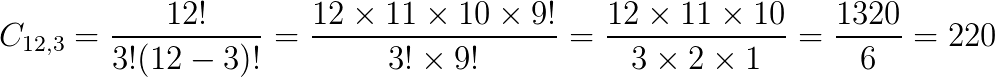
Podemos separar as 12 bolas de gudes distintas, com três em cada pote, de 220 formas diferentes.
Combinação com repetição
Utilizamos a combinação com repetição quando a ordem dos elementos do evento não importa, porém, podemos escolher cada elementos mais de uma vez.
Para calcular uma combinação com repetição usamos a seguinte fórmula:
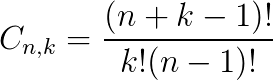
Onde:
- Cn,k: é a combinação com repetição;
- n: é o total de elementos do evento;
- k: total de elementos escolhidos do evento.
Exemplo:
Uma loja decide sortear para os clientes 3 pares de sapatos das 10 melhores marcas do mercado. De quantas formas o ganhador do prêmio pode escolher os três pares de sapatos da lista das 10 melhores marcas, sendo permitido repetições?
Resolução:
Temos os seguintes dados:
- n: 10 marcas;
- k: 3 pares de sapatos.
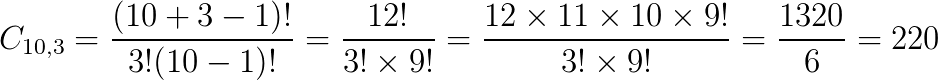
Portanto, o ganhador do prêmio poderá escolher de 220 maneiras distintas os três pares de sapatos das 10 melhores marcas.
Permutação, Arranjo e Combinação são os assuntos da análise combinatória que aparecem com muita frequência em problemas de concursos e do Enem. Portanto, estude, pratique e boa sorte!
Exercícios
Veja os exercícios no link a seguir:



