Fatorial: Definição e Operações Com Exemplos

Fatorial é o produto dos números inteiros positivos consecutivos de um número natural n, menores ou iguais a n. A notação do fatorial de um número n é: n!.

Definição

Seja n um número natural, o fatorial de n é definido por:

• 0! = 1
• n! = n . (n – 1).(n – 2) … 3 . 2 . 1

Exemplos

• Como se ler:
  • n!: fatorial de n;
  • 1!: fatorial de 1;
  • 5!: fatorial de 5.
• Exemplos:
  • 0: 0! = 1
  • 1: 1! = 1
  • 2: 2! = 2 . 1 = 2
  • 3: 3! = 3 . 2 . 1 = 6
  • 4: 4! = 4 . 3 . 2 . 1 = 24
  • 5: 5! = 5 . 4 . 3 . 2 . 1 = 120
  • 6: 6! = 6 . 5 . 4 . 3 . 2 . 1 = 720
  • 7: 7! = 7 . 6 . 5 . 4 . 3 . 2 . 1 = 5.040
  • 8: 8! = 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 40.320
  • 9: 9! = 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 362.880
  • 10: 10! = 10 . 9 . 8 . 7 . 6 . 5 . 4. 3 . 2 . 1 = 3.628.800

Análise Combinatória

Na análise combinatória é frequentemente usado fatoriais nos problemas envolvendo arranjos, combinações e permutações de elementos de um conjunto finito.

Fórmulas com fatoriais na análise combinatória

Arranjos

Arranjo é a quantidade de agrupamentos possíveis que podemos realizar em um conjunto finito:

Fórmula:

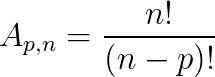
Combinações

Combinação é um agrupamento de elementos de uma conjunto em subconjuntos.

Fórmula:

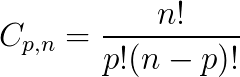
Permutações

Permutação é uma ordenação de objetos distintos de um conjunto em ordens diferentes.

Fórmula:

P_n = n!

Equação de Fatorial

Podemos muito bem encontrar em problemas matemáticos equações envolvendo números fatoriais. Dessa forma, ao resolver a equação é preciso resolver também o fatorial.

Exemplo de equações:

• Equação 1:
  • x + 2 = 5! ⇒
  • x + 2 = 120 ⇒
  • x + = 120 – 2 ⇒
  • x = 118
• Equação 2:
  • y – 4 = 2! ⇒
  • y – 4 = 2 ⇒
  • y = 2 + 4 ⇒
  • y = 6
• Equação 3:
  • x – 4! = 2 ⇒
  • x – 24 = 2 ⇒
  • x = 2 + 24 ⇒
  • x = 26

Operações com Fatoriais

Podemos aplicar as quatro operações básicas em números fatoriais, para resolver as operações é preciso desenvolver os fatoriais realizando o produto. Veja como fazer:

Adição

• 2! + 5! ⇒
• (2 . 1) + (5 . 4 . 3 . 2 . 1) ⇒
• 2 + 120 = 122

Subtração

• 4! – 3! ⇒
• (4 . 3 . 2 . 1) – (3 . 2 . 1) ⇒
• 24 – 6 = 18

Multiplicação

• 3! . 1! ⇒
• (3 . 2 . 1) . (1) ⇒
• 6 . 1 = 6

Divisão

Simplificação de Fatoriais

A simplificação de fatoriais é possível quando dividimos dois números fatoriais. Dessa forma, podemos cortar os termos iguais no numerador e no denominador. Veja na imagem abaixo como fazer:

Exercícios

Veja os exercícios no link a seguir:

• Exercícios sobre fatorial