Treine seus conhecimentos resolvendo os exercícios a seguir sobre binômio de Newton. É importante resolver as questões sem consultar as respostas antecipadamente, tente resolver primeiro.
1) Desenvolva o binômio (x + 9)³:
Ver resposta
Desenvolvendo o binômio, temos o seguinte:
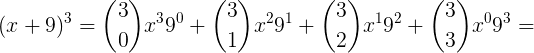
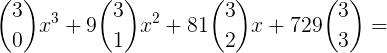
Portanto, ao resolver o binômio acima chegamos ao polinômio de grau 3 abaixo:
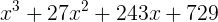
2) Dado o binômio:
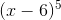
Realize a soma dos seus coeficientes após o desenvolvimento.
Ver resposta
Pelo termo geral, temos que:
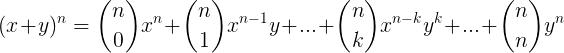
Dessa forma, temos que a soma dos coeficientes será:
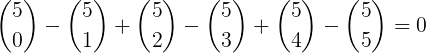
1 – 5 + 10 – 10 + 5 – 1 = 0
Portanto, a soma dos coeficientes do binômio dado na questão é igual a 0.
3) Determine o 5º termo desenvolvimento do binômio :
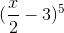
Ver resposta
Aplicando a fórmula, temos o seguinte:
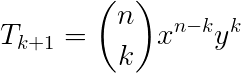
Temos:
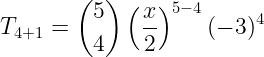
Então:
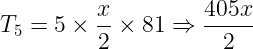
4) Seja o binômio:
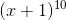
, determine o termo independente do desenvolvimento.
Ver resposta
Aplicando a fórmula do termo independente, temos:
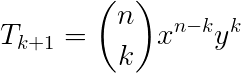
Substituindo o valor de n, assim:
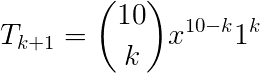
O termo independente é aquele em que x seja elevado a zero.
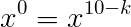
Eliminando as bases, temos:
10 – k = 0 ⇒ k = 10
Agora, calculando o termo independente, temos:
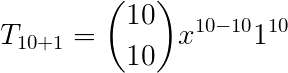
Logo:
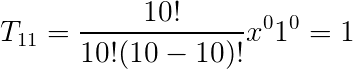
Portanto, temos que o termo independente é igual a 1.
Para ficar bom em resolver exercícios com binômio de newton é importante praticar.


