Trigonometria é a área da matemática que estuda as relações envolvendo os lados de um triângulo retângulo, que um polígono que possui três ângulos. A origem do nome vem do grego que se refere a medidas de três ângulos.
A partir dos lados do triângulo é que encontramos as razões seno, cosseno e tangente. Na Geometria também existem outras abordagens que utilizam a trigonometria, como nos estudos das esferas.
Trigonometria no triângulo retângulo
No triângulo retângulo, os ângulos notáveis (30º, 45º e 60º) possuem valores que são constantes sendo representados pelas relações seno, cosseno e tangente.
Funções trigonométricas
As funções trigonométricas, seno, cosseno e tangente, são as relações no triângulo retângulo (triângulo com um angulo que mede 90°) das razões entre os lados em função do ângulo. Podemos encontrar essas funções através dos catetos, oposto e adjacente e da hipotenusa.
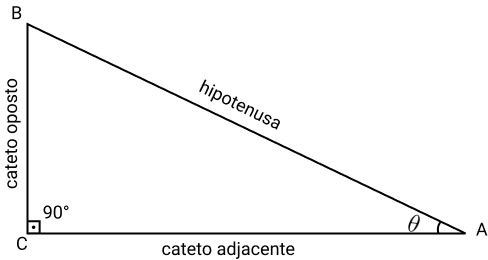
Cateto oposto
O cateto oposto é o que fica no lado oposto ao ângulo referência (θ).
Cateto adjacente
O cateto adjacente é o que está ao lado (adjacente) do ângulo de referência (θ).
Hipotenusa
A hipotenusa é o lado mais longo do triângulo, oposto ao ângulo reto.
Seno (sen)
O seno é dado pela razão do cateto oposto sobre a hipotenusa.
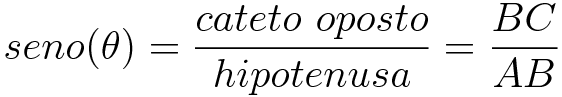
Cosseno (cos)
O cosseno é dado pela razão entre o cateto adjacente sobre a hipotenusa.
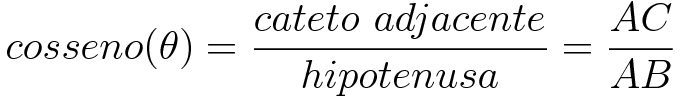
Tangente (tan ou tg)
A tangente é a razão dada pelo cateto oposto sobre a cateto adjacente.

A partir das funções trigonométricas acima, podemos encontrar outras funções trigonométricas: cotangente, cossecante e secante.
Cotangente (cot)
A cotangente é o inverso da tangente, dado pelo cateto adjacente sobre o cateto oposto, que é o mesmo que o cosseno sobre o seno.
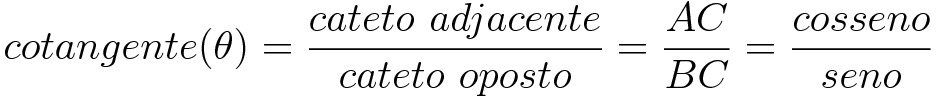
Cossecante (csc)
A cossecante é o inverso do seno, ou seja, a hipotenusa sobre o cateto oposto.
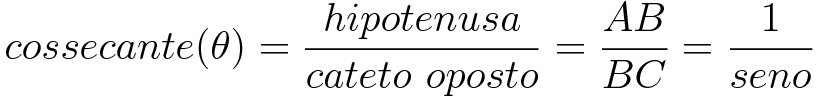
Secante (sec)
A secante é a razão dada pela hipotenusa sobre o cateto adjacente.
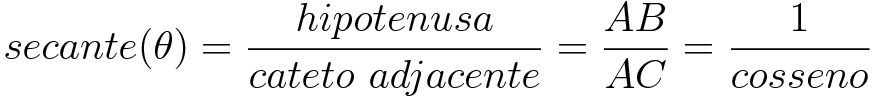
Círculo trigonométrico
O círculo trigonométrico ou ciclo trigonométrico é a disposição no plano cartesiano para facilitar a visualização das funções trigonométricas durante o estudo da trigonometria. Dessa forma, é possível visualizar graficamente durante o estudo dessas funções e poderá entender a disposição do seno, cosseno, tangente, cotangente, cossecante e secante. Veja abaixo:

Teorema de Pitágoras
O Teorema de Pitágoras define que a relação em um triângulo ABC, com ângulo reto em C, vale a seguinte relação: (AB)² = (AC)² + (BC)². Em outras palavras, Pitágoras descobriu que o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.
Considere o triângulo retângulo:

Vamos chamar os lados AB de a, BC de b e AC de c, então:
a² = b² + c²
Onde
- a é a hipotenusa;
- b é cateto oposto;
- c o cateto adjacente.
Geometria Euclidiana e Trigonometria
Euclides definiu alguns conceitos que são usados no estudo da trigonometria aplicada no triângulo.
Lei dos Senos
A Lei dos Senos serve para relacionar o seno do ângulo de um triângulo qualquer com o lado oposto a este ângulo.
Exemplo:
Considere o triângulo ABC abaixo, inscrito na circunferência, com lados a, b e c:

A lei dos senos é dada pela seguinte fórmula:
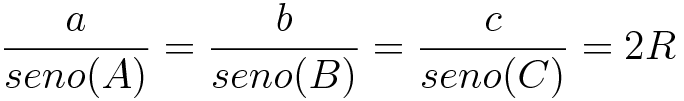
A fórmula diz que a razão entre um lado qualquer do triângulo e o seno do ângulo oposto a este lado, é igual a 2 vezes o tamanho do raio da circunferência.
Lei dos Cossenos
A Lei dos Cossenos diz que podemos encontrar a medida de um lado de um triângulo, somando as medidas dos lados opostos a ele e subtraindo pelo dobro do produto entre os opostos e o cosseno do ângulo, também dos lados contrários ao lado em questão.
Exemplo:
Considere o triângulo ABC abaixo, com lados a, b e c:
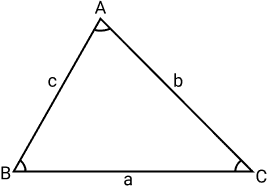
A lei dos cossenos é dada pela seguinte fórmula:
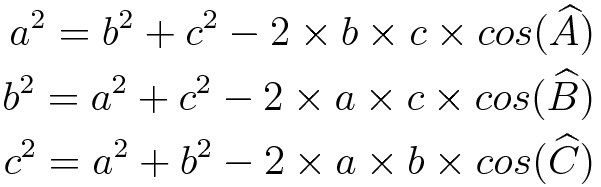
A fórmula diz que podemos encontrar a medida elevada ao quadrado de um lado do triângulo, realizando a soma dos lados opostos também ao quadrado. Após isso, subtraímos desta soma dos lados opostos ao quadrado, o produto entre as medidas dos lados opostos e o cosseno do ângulo oposto ao lado que queremos encontrar multiplicado por 2.
Lei das Tangentes
A Lei das Tangentes diz ser equivalente os comprimentos de um triângulo não isósceles com a tangente dos ângulos opostos a esses lados.
Exemplo:
Considere o triângulo ABC abaixo, inscrito na circunferência, com lados a, b e c:

A lei dos tangentes é dada pela seguinte fórmula:
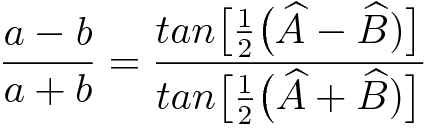
Exercícios de trigonometria
Veja os exercícios acessando o link a seguir:
É isso aí!


