A Lei dos Cossenos pode ser usada no cálculo da medida de um lado ou de um ângulo, desde que conheçamos as outras medidas.
O Teorema e as Fórmulas da Lei dos Cossenos
A Lei dos Cossenos é uma generalização do Teorema de Pitágoras. O teorema da Lei dos Cossenos diz que:
“Em todo triângulo, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros lados, menos o dobro do produto dessas medidas pelo cosseno do ângulo que eles formam.”
Exemplo:
Seja o triângulo ABC a seguir:

Assim, pela lei dos cossenos temos as seguintes fórmulas:
- a² = b² + c² – 2 . b . c . cos(A)
- b² = a² + c² – 2 . a . c . cos(B)
- c² = a² + b² – 2 . a . b . cos(C)
Demonstração da Lei dos Cossenos
Considere o triângulo ABC da figura com altura h em relação ao lado AC do triângulo.
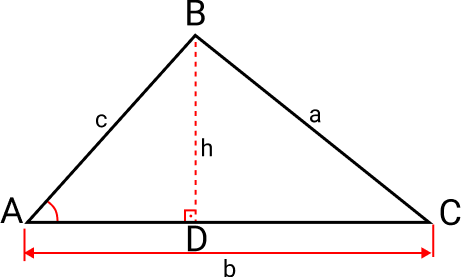
No triângulo retângulo ABD, temos o seguinte:
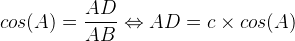
A base do triângulo, CD, temos que: CD = b – AD ⇔ CD = b – c . cos(A)
Com base nos itens anteriores, podemos aplicar o Teorema de Pitágoras: h² = c² – AD² = a² – CD².
Substituindo: CD = b – c . cos(A) em a² – CD² temos: a² – (b – c . cos(A))².
Substituindo: AD = c . cos A em c² – AD² temos: c² – (c . cos(A))².
Resolvendo, temos:
a² – (b – c . cos(A))² = c² – (c . cos(A))² ⇔ a² – b² + 2 . b . c . cos(A) – c² . cos²(A) = c² – c² . cos²(A) ⇔ a² = b² + c² – 2 . b . c . cos(A)
Analogamente, para a altura do triângulo em relação aos outros lados, temos:
- b² = a² + c² – 2 . a . c . cos(B)
- c² = a² + b² – 2 . a . b . cos(C)
A Lei dos Cossenos no Triângulo Retângulo
A Lei dos Cossenos pode ser aplicada em qualquer triângulo retângulo.
Relembrando, um triângulo retângulo possui um ângulo reto que mede 90°. E vamos aplicar a lei dos cossenos no lado oposto deste ângulo. Assim:
a² = b² + c² – 2 . b . c . cos(90)
Sabemos que o cosseno que 90° é 0. Dessa forma, a expressão acima fica assim:
a² = b² + c²
Essa expressão é o Teorema de Pitágoras. Então, podemos dizer que para o triângulo retângulo, quando queremos descobrir a medida de um lado, é melhor utilizar o Teorema de Pitágoras.
A Lei dos Cossenos, então, poderia ser utilizada para encontrar a medida de um ângulo quando conhecemos as medidas dos lados.
Exercícios Resolvidos
Seja um triângulo com dois lados medindo 15 cm e 10 cm, onde o ângulo entre esses lados mede 130°. Encontre a medida do terceiro lado.
Resolução:
Vamos utilizar a Lei dos Cossenos para encontrar a medida do terceiro lado desse triângulo.
Considerando as seguintes medidas:
- b = 15 cm
- c = 10 cm
- θ = 130° = cos(130) = -0,6
Substituindo na fórmula seguinte, pois queremos encontrar a medida de a:
- a² = b² + c² – 2 . b . c . cos(130)
- a² = 15² + 10² – 2 . 15 . 10 . (-0,6)
- a² = 225 + 100 + 180
- a² = 505
- a = √505
- a ≈ 22,5
Dessa forma, a medida do lado a é de cerca de 22,5 cm. Então, a é o lado correspondente a hipotenusa.
Seja um triângulo com dois lados medindo 10 cm e 5 cm e o ângulo ABC medindo 30°. Encontre a medida do terceiro lado e a média do ângulo ACB.
Resolução:
Considerando as seguintes medidas:
- a = 10 cm
- c = 5 cm
- ABC = θ = 30° = cos(30) = 0,87
Vamos encontra a medida de b:
- b² = a² + c² – 2 . a . c . cos(B)
- b² = 10² + 5² – 2 . 10 . 5 . cos(30)
- b² = 100 + 25 – 2 . 10 . 5 . 0,87
- b² = 125 – 87
- b² = 38
- b = √38
- b ≈ 6,16
Assim, a medida do lado b é de aproximadamente 6,16 cm. Vamos medir o ângulo ACB:
- c² = a² + b² – 2 . a . b . cos(C)
- 5² = 10² + (6,16)² – 2 . 10 . 6,16 . cos(C)
- 25 = 100 + 37,95 – 123,2 . cos(C)
- 25 – 100 – 37,95 = – 123,2 . cos(C)
- -112,95 = – 123,2 . cos(C) -112,95 / – 123,2 = cos(C)
- cos(C) = 0,92
O cosseno de 23° é 0,92, dessa forma o ângulo ACB mede 23°.
Exercícios de trigonometria
Veja os exercícios no link abaixo:



