A Lei dos Senos estabelece que em um triângulo qualquer, as medidas dos lados são proporcionais aos senos ângulos opostos.
Além disso, um triângulo circunscrito numa circunferência de raio r, a medida do diâmetro da circunferência é a razão de proporcionalidade.
Exemplo:
Seja o triângulo ABC de lados a, b e c, inscrito na circunferência de raio r e centro O:
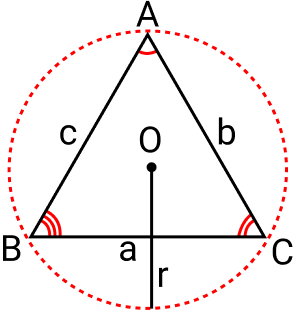
Assim, temos que as seguintes relações são válidas:
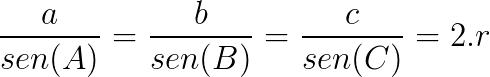
Demonstração da Lei dos Senos
Vamos demonstrar a Lei dos Senos considerando um triângulo ABC, inscrito numa circunferência de raio r.
Desenhando uma reta a partir de B, passando pelo centro O até chegar a linha da circunferência que chamaremos ponto D.
Desenhando outra reta de D até o ponto C, formaremos um triângulo retângulo BCD. Com ângulo reto em C.
Conforme a figura a seguir:
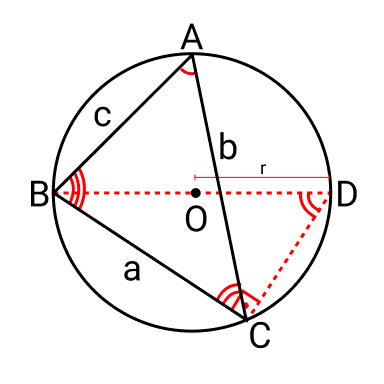
Analisando a figura acima, temos que:
Se BD = 2.r é diâmetro da circunferência, então podemos concluir que C = 90°. Dessa forma,
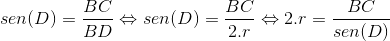
Ainda analisando a figura, e conforme o teorema do ângulo inscrito, BAC = BDC, pois são ângulos inscritos na circunferência no mesmo arco. Logo, sen(D) = sen(A).
Pelos itens acima, temos que:
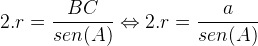
Da mesma forma, podemos afirmar que:
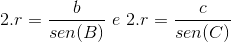
E assim, conclui-se que:
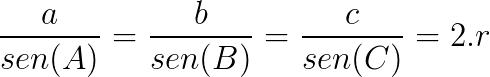
Aplicação da Lei dos Senos
A Lei dos Senos é utilizada para encontrar as medidas dos lados de um triângulo e também dos ângulos.
Exemplo:
Considere o triângulo ABC a seguir de lados a, b e c medindo 10 cm:

Assim, utilizando a lei dos senos podemos estabelecer a seguinte relação:
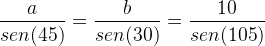
Lembre-se que a soma interna dos ângulos de um triângulo é igual a 180°.
Podemos estabelecer as medidas para a e b da seguinte forma:
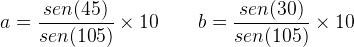
Portanto, as medidas de a = 5,18 e b = 7,32
Para encontrarmos as medidas dos lados de um triângulo, é necessário apenas conhecermos as medidas dos seus ângulos e apenas a medida de um de seus lados.
A Lei dos Senos no Triângulo Retângulo
Considere o triângulo retângulo ABC a seguir, reto em C.
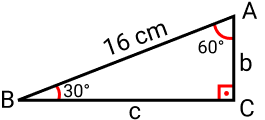
Agora vamos utilizar a lei para encontrar as medidas dos lados b e c do triângulo acima.
Como sabemos, com a lei dos senos nós precisamos apenas das medidas dos ângulos e conhecer apenas a medida de um lado. Isso é suficiente para encontrarmos as medidas dos lados restantes.
Dessa forma, ao aplicarmos a lei temos a seguinte relação:
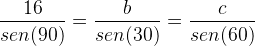
Agora vamos estabelecer as médias para os lados b e c da seguinte forma:
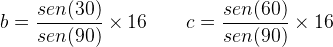
Portanto, as medidas de b = 8 e c = 13,86
Exercícios de trigonometria
Veja os exercícios no link abaixo:



