As razões trigonométricas no triângulo retângulo são as relações estabelecidas entre os ângulos do triângulo. Essas relações são obtidas através da divisão entre os valores correspondentes aos lados do triângulo.
Triângulo Retângulo
O triângulo retângulo recebe esse nome porque possui um ângulo reto, isto é, um ângulo que mede 90°.
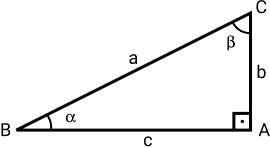
A soma dos ângulos internos no triângulo retângulo é igual a 180°. Então, para o triangulo ABC acima apresentado, temos que:
α + β + 90° = 180° ⇒ α + β = 90°
Dessa forma, concluímos que:
- Os ângulos α e β são chamados de ângulos complementares, isto é, são os ângulos em que suas medidas somam 90°;
- Os ângulos complementares devem medir, necessariamente, menos que 90°.
O triângulo retângulo tem um ângulo reto e dois que são complementares entre si. Os lados b e c são chamados de catetos e a é a hipotenusa. Sendo que a hipotenusa é sempre oposta ao ângulo reto do triângulo e maior que os catetos, como mostra o Teorema de Pitágoras.
Razões Trigonométricas no Triângulo Retângulo
As principais razões trigonométricas são: seno, cosseno e a tangente. Essas razões ou relações trigonométricas são válidas em qualquer triângulo retângulo.
Assim, definiremos o seno, cosseno e a tangente de um ângulo agudo em um triângulo retângulo pelas relações apresentada a seguir:

O seno, cosseno e a tangente são funções dos ângulos internos do triângulo retângulo e não dos lados.
Cotangente, Secante e Cossecante
Além das razões trigonométricas definidas anteriormente, podemos definir também por meio dos lados do triângulo a cotangente, a secante e a cossecante. Veja:

Tabela de Razões Trigonométricas
A tabela trigonométrica para todos os valores dos senos, cossenos e para as tangentes de todos os ângulos do triângulo retângulo é apresentada a seguir:
| Ângulos (Grau) | Seno | Cosseno | Tangente |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 1° | 0,0175 | 0,9998 | 0,0175 |
| 2° | 0,0349 | 0,9994 | 0,0349 |
| 3° | 0,0523 | 0,9986 | 0,0524 |
| 4° | 0,0698 | 0,9976 | 0,0699 |
| 5° | 0,0872 | 0,9962 | 0,0875 |
| 6° | 0,1045 | 0,9945 | 0,1051 |
| 7° | 0,1219 | 0,9925 | 0,1228 |
| 8° | 0,1392 | 0,9903 | 0,1405 |
| 9° | 0,1564 | 0,9877 | 0,1584 |
| 10° | 0,1736 | 0,9848 | 0,1763 |
| 11° | 0,1908 | 0,9816 | 0,1944 |
| 12° | 0,2079 | 0,9781 | 0,2126 |
| 13° | 0,2250 | 0,9744 | 0,2309 |
| 14° | 0,2419 | 0,9703 | 0,2493 |
| 15° | 0,2588 | 0,9659 | 0,2679 |
| 16° | 0,2756 | 0,9613 | 0,2867 |
| 17° | 0,2924 | 0,9563 | 0,3057 |
| 18° | 0,3090 | 0,9511 | 0,3249 |
| 19° | 0,3256 | 0,9455 | 0,3443 |
| 20° | 0,3420 | 0,9397 | 0,3640 |
| 21° | 0,3584 | 0,9336 | 0,3839 |
| 22° | 0,3746 | 0,9272 | 0,4040 |
| 23° | 0,3907 | 0,9205 | 0,4245 |
| 24° | 0,4067 | 0,9135 | 0,4452 |
| 25° | 0,4226 | 0,9063 | 0,4663 |
| 26° | 0,4384 | 0,8988 | 0,4877 |
| 27° | 0,4540 | 0,8910 | 0,5095 |
| 28° | 0,4695 | 0,8829 | 0,5317 |
| 29° | 0,4848 | 0,8746 | 0,5543 |
| 30° | 0,5000 | 0,8660 | 0,5774 |
| 31° | 0,5150 | 0,8572 | 0,6009 |
| 32° | 0,5299 | 0,8480 | 0,6249 |
| 33° | 0,5446 | 0,8387 | 0,6494 |
| 34° | 0,5592 | 0,8290 | 0,6745 |
| 35° | 0,5736 | 0,8192 | 0,7002 |
| 36° | 0,5878 | 0,8090 | 0,7265 |
| 37° | 0,6018 | 0,7986 | 0,7536 |
| 38° | 0,6157 | 0,7880 | 0,7813 |
| 39° | 0,6293 | 0,7771 | 0,8098 |
| 40° | 0,6428 | 0,7660 | 0,8391 |
| 41° | 0,6561 | 0,7547 | 0,8693 |
| 42° | 0,6691 | 0,7431 | 0,9004 |
| 43° | 0,6820 | 0,7314 | 0,9325 |
| 44° | 0,6947 | 0,7193 | 0,9657 |
| 45° | 0,7071 | 0,7071 | 1 |
| 46° | 0,7193 | 0,6947 | 1,0355 |
| 47° | 0,7314 | 0,6820 | 1,0724 |
| 48° | 0,7431 | 0,6691 | 1,1106 |
| 49° | 0,7547 | 0,6561 | 1,1504 |
| 50° | 0,7660 | 0,6428 | 1,1918 |
| 51° | 0,7771 | 0,6293 | 1,2349 |
| 52° | 0,7880 | 0,6157 | 1,2799 |
| 53° | 0,7986 | 0,6018 | 1,3270 |
| 54° | 0,8090 | 0,5878 | 1,3764 |
| 55° | 0,8192 | 0,5736 | 1,4281 |
| 56° | 0,8290 | 0,5592 | 1,4826 |
| 57° | 0,8387 | 0,5446 | 1,5399 |
| 58° | 0,8480 | 0,5299 | 1,6003 |
| 59° | 0,8572 | 0,5150 | 1,6643 |
| 60° | 0,8660 | 0,5000 | 1,7321 |
| 61° | 0,8746 | 0,4848 | 1,8040 |
| 62° | 0,8829 | 0,4695 | 1,8807 |
| 63° | 0,8910 | 0,4540 | 1,9626 |
| 64° | 0,8988 | 0,4384 | 2,0503 |
| 65° | 0,9063 | 0,4226 | 2,1445 |
| 66° | 0,9135 | 0,4067 | 2,2460 |
| 67° | 0,9205 | 0,3907 | 2,3559 |
| 68° | 0,9272 | 0,3746 | 2,4751 |
| 69° | 0,9336 | 0,3584 | 2,6051 |
| 70° | 0,9397 | 0,3420 | 2,7475 |
| 71° | 0,9455 | 0,3256 | 2,9042 |
| 72° | 0,9511 | 0,3090 | 3,0777 |
| 73° | 0,9563 | 0,2924 | 3,2709 |
| 74° | 0,9613 | 0,2756 | 3,4874 |
| 75° | 0,9659 | 0,2588 | 3,7321 |
| 76° | 0,9703 | 0,2419 | 4,0108 |
| 77° | 0,9744 | 0,2250 | 4,3315 |
| 78° | 0,9781 | 0,2079 | 4,7046 |
| 79° | 0,9816 | 0,1908 | 5,1446 |
| 80° | 0,9848 | 0,1736 | 5,6713 |
| 81° | 0,9877 | 0,1564 | 6,3138 |
| 82° | 0,9903 | 0,1392 | 7,1154 |
| 83° | 0,9925 | 0,1219 | 8,1443 |
| 84° | 0,9945 | 0,1045 | 9,5144 |
| 85° | 0,9962 | 0,0872 | 11,4301 |
| 86° | 0,9976 | 0,0698 | 14,3007 |
| 87° | 0,9986 | 0,0523 | 19,0811 |
| 88° | 0,9994 | 0,0349 | 28,6363 |
| 89° | 0,9998 | 0,0175 | 57,2900 |
| 90° | 1 | 0 | ___ |
Ângulos Notáveis
Em muitos problemas envolvendo trigonometria, três tipos de ângulos aparecem com maior frequência aplicado no estudo das razões trigonométricas. São eles: 30°, 45° e 60°.
Esses ângulos são chamados de ângulos notáveis. A tabela a seguir apresenta os valores para o seno, cosseno e para a tangente dos ângulos notáveis:
| Relações Trigonométricas | 30° | 45º | 60° |
|---|---|---|---|
| Seno | 1/2 | √2/2 | √3/2 |
| Cosseno | √3/2 | √2/2 | 1/2 |
| Tangente | √3/3 | 1 | √3 |
Aplicação das Razões Trigonométricas
Existem muitos problemas na engenharia que podem ser aplicadas as razões trigonométricas para resolver um determinado problema real.
Exemplo:
(CPCAR-MG) Um avião decola de um ponto B sob a inclinação de um ângulo de 15° com a horizontal. A 2 km de B encontra-se a projeção vertical de C do ponto mais alto D de uma serra de 600 m de altura. Conforme a figura a seguir:

Dados: cos 15° = 0,97, sen 15° = 0,26, tan 15° = 0,27
É correto afirmar que:
- a) não haverá colisão do avião com a serra;
- b) haverá colisão com a serra antes do avião alcançar 540 m de altura;
- c) haverá colisão com a serra em D;
- d) se o avião decolar 220 m antes de B mantendo a mesma inclinação, não haverá colisão do avião contra a serra.
Resolução:
A figura da questão forma um triângulo retângulo BCA, com ângulo reto em C. Onde A é o lado formado pela rota do avião.
Para responder essa questão, precisamos encontrar o valor da medida do lado CA. Essa medida é a tangente do ângulo de 15°. Logo:
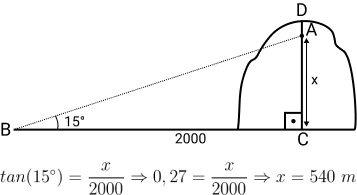
Lembrando que a tangente é o cateto oposto sobre o adjacente, ou seja, BC/AC
Segundo a questão, a altura da serra, formada pelo lado CD, possui 600 metros de altura, então haverá colisão com a serra antes do avião alcançar 540 m de altura. Resposta B.
Exercícios de trigonometria
Acesse os exercícios no link a seguir:


