Os ângulos notáveis são os ângulos de 30°, 45° e 60°. Eles recebem esse nome devido à frequência com que aparecem em problemas matemáticos.
Tabela dos Ângulos Notáveis
Para facilitar o cálculo e para quem não consegue memorizar, podemos utilizar uma tabela contendo os valores do seno, cosseno e da tangente para esses ângulos.
| Seno | Cosseno | Tangente | |
|---|---|---|---|
| 30° | 1⁄2 | √3/2 | √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1⁄2 | √3 |
Como construir a tabela dos Ângulos Notáveis
Para construir a tabela dos ângulos notáveis, primeiro devemos criar uma tabela para preenchermos da seguinte forma:
- Na primeira linha coloquemos as razões trigonométricas.
- Na primeira coluna coloquemos os ângulos notáveis.
| Seno | Cosseno | Tangente | |
|---|---|---|---|
| 30° | |||
| 45° | |||
| 60° |
Agora, na coluna do seno coloque a sequência numérica 1, 2 e 3, em ordem crescente, começando a partir do ângulo de 30°.
| Seno | Cosseno | Tangente | |
|---|---|---|---|
| 30° | 1 | ||
| 45° | 2 | ||
| 60° | 3 |
Na coluna do cosseno, coloque a mesma sequência, mas agora em ordem decrescente.
| Seno | Cosseno | Tangente | |
|---|---|---|---|
| 30° | 1 | 3 | |
| 45° | 2 | 2 | |
| 60° | 3 | 1 |
Nesta etapa, coloque o símbolo raiz, exceto no número 1. Veja:
| Seno | Cosseno | Tangente | |
|---|---|---|---|
| 30° | 1 | √3 | |
| 45° | √2 | √2 | |
| 60° | √3 | 1 |
Nesse passo, coloque em forma de fração adicionando no denominador o número 2.
| Seno | Cosseno | Tangente | |
|---|---|---|---|
| 30° | 1⁄2 | √3/2 | |
| 45° | √2/2 | √2/2 | |
| 60° | √3/2 | 1⁄2 |
Para finalizar, vamos preencher na tabela a coluna da tangente. É um pouco diferente. Mas não é difícil.
Vamos colocar a sequência 3, 1 e 3, a partir do ângulo de 30°. Veja:
| Seno | Cosseno | Tangente | |
|---|---|---|---|
| 30° | 1⁄2 | √3/2 | 3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1⁄2 | 3 |
Agora, nos números 3 adicionamos a raiz.
| Seno | Cosseno | Tangente | |
|---|---|---|---|
| 30° | 1⁄2 | √3/2 | √3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1⁄2 | √3 |
Para finalizar, na primeira linha da tangente coloquemos √3 com o denominador 3.
| Seno | Cosseno | Tangente | |
|---|---|---|---|
| 30° | 1⁄2 | √3/2 | √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1⁄2 | √3 |
Essa é a tabela dos ângulos notáveis.
Como calcular o seno, o cosseno e a tangente dos ângulos de 30° e 60° no triângulo retângulo?
Para construir a tabela acima precisamos entender como calcular a seno e o cosseno dos ângulos de 30° e 60° no triângulo retângulo.
Considere o triângulo ABC da figura a seguir:
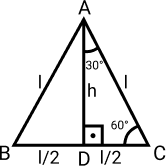
Primeiramente, vamos calcular a medida da altura h utilizando o teorema de Pitágoras.
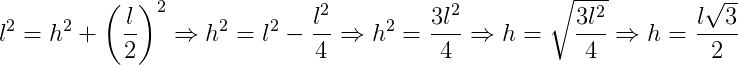
O seno de 30° é a razão entre o cateto oposto e a hipotenusa. Da mesma forma, o seno de 60° é a razão entre cateto oposto e a hipotenusa.
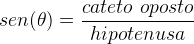
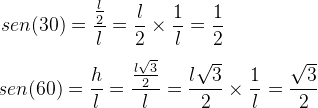
Cosseno de 30° é a razão entre o cateto adjacente e a hipotenusa. Assim como o cosseno de 60° também é a razão entre o cateto adjacente e a hipotenusa.
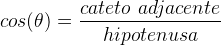
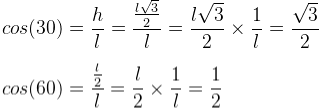
A tangente de um ângulo é a razão entre o cateto oposto e o adjacente no triângulo retângulo.
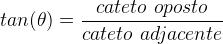
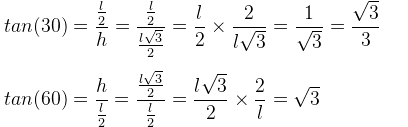
Na tangente de 30° obtemos √3 no denominador, neste caso fizemos uma racionalização de denominadores, ou seja, tiramos a raiz do denominador para simplificar. Para entender esse processo veja aqui.
Como calcular o seno, o cosseno e a tangente de 45° no triângulo retângulo?
Para calcular o seno e o cosseno do ângulo de 45° vamos usar como exemplo o quadrado da figura abaixo.
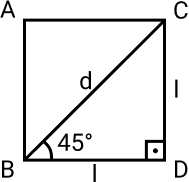
Se traçarmos uma reta do vértice B ao vértice C, temos uma diagonal d que corta o quadrado formando dois triângulos retângulos com ângulos complementares de 45°.
Dessa forma, utilizando o Teorema de Pitágoras, a diagonal d pode ser escrita em função dos lados da seguinte forma:
- d² = l² + l² ⇒
- d² = 2l² ⇒
- d = l√2
Como já sabemos, o seno de um ângulo é a razão entre o cateto oposto e a hipotenusa. Então, o seno de 45° na diagonal acima é:
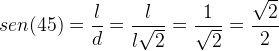
Da mesma forma, o cosseno de um ângulo é a razão entre o cateto adjacente e a hipotenusa. Então, o cosseno de 45° é:
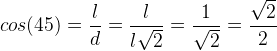
A tangente de 45° é a razão entre o cateto oposto e o cateto adjacente. Assim:
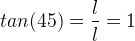
Exercícios
Veja os exercícios acessando o link a seguir:



