Racionalização de denominadores é uma técnica para tornar frações com denominadores irracionais em racionais.
As frações cujo denominador é uma raiz, podem ser transformadas em uma fração com denominador que não seja uma raiz, sem alterar o seu resultado.
Utilizamos a técnica de racionalização de denominadores para facilitar o cálculo, pois trabalhar com números irracionais é um pouco complicado. Além disso, números irracionais apresentam pouca precisão no resultado.
Multiplicaremos o numerador e denominador pelo mesmo número com a finalidade de eliminar a raiz do denominador. Esse processo transformará uma fração com denominador irracional em uma fração equivalente.
Racionalizando denominadores de uma fração
Para racionalizar denominadores precisamos eliminar o denominador irracional, faremos isso conhecendo alguns métodos do mais simples para os mais complexos.
Racionalização de Denominadores com uma Raiz Quadrada
Racionalizar uma fração com raiz quadrada no denominador é o caso mais simples.
Exemplo:
Considere a seguinte fração:
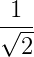
Para racionalizar frações com denominadores que são raízes quadradas, devemos multiplicar toda a fração pela mesma raiz quadrada do denominador. Assim:
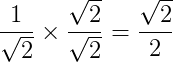
Nesse caso, dizemos que √2 é o fator racionalizante da fração.
Conforme a propriedade de radiciação, eliminamos a raiz quadrada multiplicando a raiz por ela mesma, pois √2 . √2 = 2.
Exemplo:
Considere a seguinte fração:
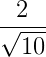
Da mesma forma, racionalizá-la é multiplicar toda a fração por √10, assim:
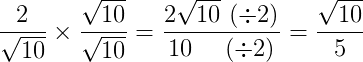
Bom, como você já viu, caro leitor, racionalizar frações com raiz quadrada é extremamente simples. Vamos agora ver quando a fração não possui um denominador com uma raiz quadrada.
Racionalização de Denominadores com uma Raiz não Quadrada
Para as frações cujos denominadores não são raízes quadradas, isto é, quando o índice não é 2, temos que seguir a seguinte regra:
Quando multiplicarmos uma fração com denominador:
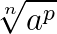
Devemos multiplicar o numerador e denominador da fração por:
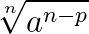
pois,
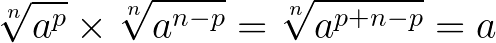
Exemplo:
Considere a seguinte fração:

Onde:
- n = 5;
- p = 2.
Nessa passo é importante saber as propriedades de radiciação.
Quando temos uma fração um denominador com uma soma ou subtração, o fator racionalizante é o seguinte:
- √a – √b o fator racionalizante é √a + √b;
- √a + √b o fator racionalizante é √a – √b;
- √a + b o fator racionalizante é √a – b;
- √a – b o fator racionalizante é √a + b;
- a + √b o fator racionalizante é a – √b;
- a – √b o fator racionalizante é a + √b;
Ou seja, quando temos uma soma ou subtração no denominador, o fator racionalizante é o mesmo denominador com a operação inversa. Se for uma soma trocamos o sinal para a subtração e vice-versa.
Exemplo:
Considere a seguinte fração:
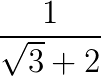
Racionalizar o denominador dessa fração é multiplicar o numerador e denominador por √3 – 2, assim:
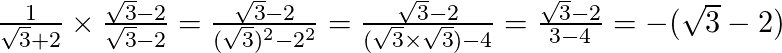
Se tivermos uma fração cujo denominador é uma soma ou subtração, sendo um dos dois uma raiz cúbica, devemos multiplicar o numerador e denominador obedecendo o seguinte:
- Se for uma soma: a² – ab + b²;
- Se for uma subtração: a² + ab + b².
Exemplo:
Considere a fração a seguir:
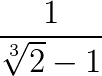
Vamos racionalizá-la seguindo as regras acima, assim:
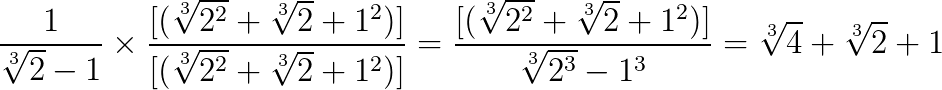
Veja como multiplicamos o denominador fazendo a distributiva:
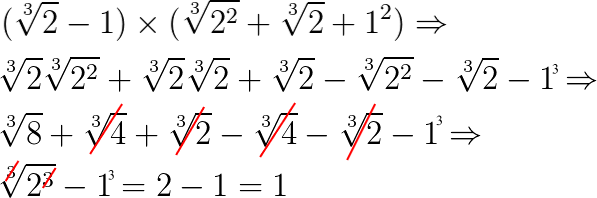
Lembrando que 8 = 2³.
Lembrete:
- a³ + b³ = (a + b)(a² – ab + b²);
- a³ – b³ = (a – b)(a² + ab + b²).



