Os produtos notáveis são expressões algébricas que aparecem com muita frequência no cálculo algébrico. São utilizados no processo de fatoração de polinômios no processo de simplificação dos mesmos.
Os produtos notáveis que vamos estudar são:
- O quadrado da soma de dois termos;
- O quadrado da diferença de dois termos;
- O produto da soma pela diferença de dois temos;
- O cubo da soma de dois termos;
- O cubo da diferença de dois termos.
Alguns conceitos que estão acima precisam ficar mais claros:
- Quadrado: quando elevamos ao expoente 2;
- Cubo: quando elevamos ao expoente 3;
- Diferença: quando subtraímos duas ou mais coisas;
- Produto: quando multiplicamos duas ou mais coisas.
Propriedades dos Produtos Notáveis
Vamos entender passo a passo cada um dos produtos notáveis.
O quadrado da soma de dois termos
O quadrado da soma de dois termos utiliza-se da potenciação para elevar a soma de dois termos ao quadrado. Assim, temos a seguinte expressão:
(a + b)² = (a + b) . (a + b)
Onde:
- a: representa o primeiro termo da expressão;
- b: representa o segundo termo da expressão.
Utilizando a propriedade distributiva da multiplicação, podemos mostrar que o quadrado da soma de dois termos é a primeiro termo ao quadrado, mais a soma dos produtos do primeiro termo com o segundo, mais o segundo termo ao quadrado.
Então, temos que:
(a + b)² = (a + b) . (a + b) = a² + ab + ab + b² = a² + 2ab + b²
Para exemplificar melhor estude a imagem abaixo e veja como funciona:
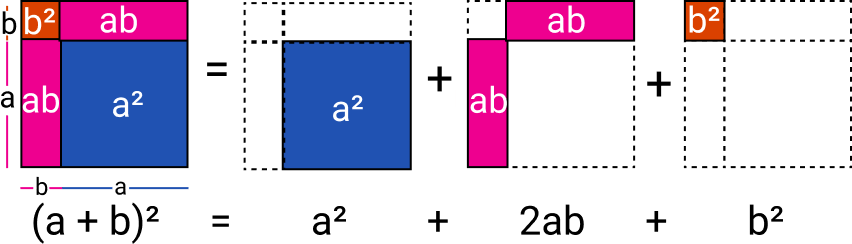
A área de um quadrado é a medida do lado elevado ao quadrado. A área de um retângulo é a multiplicação da medida de dois dos seus lados.
O quadrado da diferença de dois termos
O quadrado da diferença de dois termos também que se utiliza da potenciação para elevar a subtração de dois termos ao quadrado. Então, temos a seguinte expressão:
(a – b)² = (a – b) . (a – b)
Onde:
- a: representa o primeiro;
- b: representa o segundo.
Utilizando os conhecimentos da potenciação e da multiplicação, mais precisamente da propriedade distributiva, vamos desenvolver o problema.
Então:
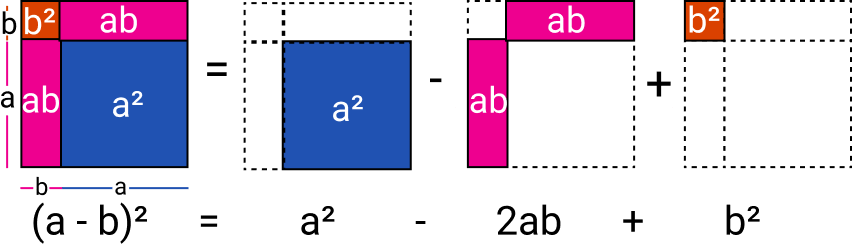
(a – b)² = (a – b) . (a – b) = a² – ab – ab + b² = a² – 2ab + b²
Assim, o quadrado da diferença de dois termos é o primeiro termo ao quadrado, pela diferença de duas vezes o produto do primeiro termo com o segundo, mais o segundo termo ao quadrado.
Pela imagem podemos entender melhor:
O produto da soma pela diferença de dois temos
O produto da soma de dois termos pela diferença ocorre quando multiplicamos uma soma entre dois termos com a subtração entre outros dois termos. Então, temos a seguinte expressão:
(a + b) . (a – b)
Assim:
(a + b).(a – b) = a² – ab + ab – b² = a² – b²
O produto da soma pela diferença é o primeiro termo ao quadrado menos o segundo termo ao quadrado. Veja na imagem para entender melhor:

O cubo da soma de dois termos
O cubo da soma de dois termos já fica um pouco mais complexo para entender. É a soma de dois termos elevado a potência de 3.
Para facilitar vamos exemplificar mostrando as potências:
(a + b)³ = (a + b).(a + b).(a + b)
ou
(a + b)³ = (a + b)².(a + b)
Então:
(a + b)³ = (a + b) . (a² + 2ab + b²) = a³ + 3a²b + 3ab² + b³
O cubo da soma de dois termos é o primeiro termo ao cubo, mais 3 vezes o primeiro termo ao quadrado vezes o segundo termo, mais 3 vezes o primeiro termo vezes o segundo termo ao quadrado, mais o segundo termo ao cubo.
Para entender melhor veja a imagem:

Lembrando que a área do cubo é o valor de seu lado elevado a 3.
O cubo da diferença de dois termos
O cubo da diferença de dois termos utiliza-se também a potenciação para elevar ao expoente 3 a subtração de dois termos.
Para facilitar vamos exemplificar mostrando as potências:
(a – b)³ = (a – b).(a – b).(a – b)
ou
(a – b)³ = (a – b)².(a – b)
Então, chegaremos a seguinte expressão:
(a – b)³ = (a – b) . (a² – 2ab + b²) = a³ – 3a²b + 3ab² – b³
O cubo da diferença de dois termos é o primeiro termo ao cubo, menos 3 vezes o primeiro termo ao quadrado vezes o segundo termo, mais 3 vezes o primeiro termo vezes o segundo termo ao quadrado, menos o segundo termo ao cubo.
A imagem do exemplo do cubo da soma de dois termos é a mesma desse, só muda o sinal.
Exercícios
Veja os exercícios no link a seguir:


