Os números decimais são os números que têm vírgula e números após essa vírgula. Os número após a vírgula são chamados de casas decimais. Os decimais estão contidos no conjuntos dos números racionais (Q).
Um número decimal pode ser negativo ou positivo. Além disso, eles podem ser finitos ou infinitos ou periódicos e infinitos. Podendo ser representado, também, na forma de uma fração.
Casa Decimal
Nos números decimais, os números que ficam após a vírgula são chamados de casas decimais.
Exemplo:
- 0,3 é um número decimal com 1 casa decimal após a vírgula.
- 1,33333… é um número decimal periódico com infinitas casas decimais após a vírgula.
Posição dos números decimais após a vírgula
Nós podemos identificar as casas decimais após a vírgula da seguinte maneira:
Considere o número decimal: 1,2645
Temos 4 algarismos após a vírgula: 2, 6, 4 e 5
Então:
- 0,2 é a posição do número decimal 2 no número acima.
- 0,06 é a posição do número 6.
- 0,004 é a posição do 4.
- 0,0005 é a posição do número 5.
Exemplo
- Número decimal finito:
- 1,3
- -2,15
- 3,25
- 0,3
- 0,5
- Número decimal infinito:
- 1,2323243244535345...
- 321,112223235565949…
- -5,223232134575656…
- Numero decimal periódico infinito:
- 1,3333333333…
- 2,1212121212…
- -9,111111111…
Números Fracionários
Os números fracionários são números decimais escritos na forma de fração.
Exemplo:
- 1⁄2 é uma fração equivalente ao decimal 0,5.
- 1⁄3 é uma fração equivalente ao número decimal periódico 0,33333…
- 1⁄4 é uma fração equivalente ao decimal 0,25.
Dízimas Periódicas e Decimais Infinitos
Alguns decimais são infinitos, dentre esses números infinitos existem uma classe chamada de dízimas periódicas por apresentarem um período que se repetem infinitamente após a vírgula.
Os números que não possuem um período que se repetem são apenas decimais infinitos.
Exemplo:
- 1,233434657… é apenas um decimal infinito.
- 10,231231231… é uma dízima periódica, com período 0,231.
Já os números que apresentam um período após a vírgula, que se repetem infinitamente, são chamados de decimais periódicos infinitos.
Exemplo:
- 1,333333… é uma dízima periódica, com período 3 que se repete.
- 0,166666666… possui um período se repetindo.
Como Ler um Número Decimal?
São lidos de acordo com a posição das casas decimais. Se possuir um número inteiro ele deve ser lido junto com a quantidade de casas decimais da parte fracionária.
Nomenclatura:
| Valor | Nome | Casas Decimais |
|---|---|---|
| 10−1 | Décimo | 1 |
| 10−2 | Centésimo | 2 |
| 10−3 | Milésimo | 3 |
| 10−4 | Décimo de Milésimo | 4 |
| 10−5 | Centésimo de Milésimos | 5 |
| 10−6 | Milionésimo | 6 |
Perceba que um número decimal pode ser escrito com uma base 10 elevado a um expoente negativo. Esse expoente equivale a quantidade de casas decimais após a vírgula.
Exemplo:
- 0,2: dois décimos.
- 3,12: três inteiros e 12 centésimos
- 0,223: duzentos e vinte e três milésimos
Operações Aritméticas
Os operações devem ser feitas com cuidado para obter o resultado correto. Veja abaixo como realizar cada uma das operações da aritmética:
Adição e Subtração
Adição: para somar dois ou mais números decimais devemos colocar números inteiros sobre inteiros, vírgula sobre vírgula e os decimais sobre os decimais.
Exemplo:
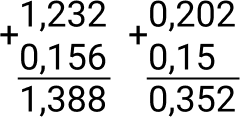
Subtração: para subtrair dois números decimais devemos escolher o maior número e subtrair pelo menor, e o procedimento é análogo a adição.
Exemplo:
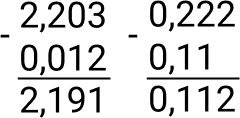
Multiplicação e Divisão
Multiplicação: para multiplicar dois ou mais números decimais, não precisamos atentar para a posição da vírgula. Devemos proceder como a multiplicação de dois ou mais números quaisquer.
Após realizar a multiplicação é que vamos contar a quantidade de casas decimais e colocar no resultado do produto.
Exemplo:
Divisão: para dividirmos números decimais precisamos verificar se os números têm as mesmas quantidades de casas decimais, caso contrário devemos completar com zeros.
Se tivermos dividindo um número inteiro por um decimal, temos que transformar o número inteiro em decimal (e vice versa), acrescentando uma vírgula e zeros após a vírgula.
Exemplo:
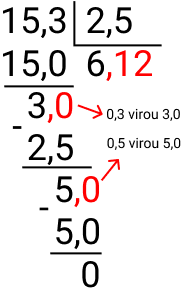
A parte em vermelho indica que o resultado da subtração foi um número menor que 2,5, para isso deslocamos a vírgula para a direita, acrescentando zeros, para que o número fosse maior que 2,5.
Curiosidade: na multiplicação de números decimais por potências de 10, 100, 1000, etc. precisamos apenas deslocar a vírgula para a direita (multiplicação) ou para a esquerda (divisão), de acordo com a quantidade de zeros que tem o número.
Exemplos:
- Multiplicação:
- 0,12 x 10 = 1,2 (deslocou a vírgula uma casa à direita)
- 1,2345 x 1000 = 1234,5 (deslocou a vírgula três casa à direita)
- Divisão:
- 0,12 ÷ 10 = 0,012 (deslocou a vírgula uma casa à esquerda)
- 1,2345 ÷ 1000 = 0,0012345 (deslocou a vírgula três casa à esquerda)
Exercícios
Veja os exercícios acessando os link a seguir:
