Multiplicação é uma das quatro operações básicas da aritmética. Consiste em uma adição sucessivas de um mesmo número produzindo um resultado que chamamos de produto.
O símbolo da multiplicação pode variar, no entanto tem o mesmo sentido: *, x ou . (ponto).
São formas de representar a multiplicação e você pode encontrá-las por aí. Dessa forma, quando encontrar uma representação da multiplicação assim já sabe do que se trata.
Na matemática, muitas vezes utiliza-se o x para representar a multiplicação, mas, para não confundir com uma variável, é frequentemente substituído pelo (.) ponto.
Numa operação utilizando a multiplicação, o multiplicador e o multiplicando são chamados de fatores, e o resultado é o produto resultante da multiplicação.
Exemplos: 10 x 2 = 20 ou 40 x 3 = 120 ou 2 . 1 = 2
Os números antes do sinal de igual são os fatores, e o valor após o sinal de igual é o produto.
Você provavelmente já deve ter ouvido por aí que a ordem dos fatores não altera o produto. Isso é verdade, veja:
Exemplos: 2 x 3 = 6 ou 3 x 2 = 6
A multiplicação nada mais é do que uma soma sucessiva de um dos fatores. A quantidade de vezes que tal fator será somado é definido pelo outro fator da operação.
Ou seja: x . y = y + y + … + y, x vezes. A quantidade de vezes que somaremos y será definido pelo número x.
No exemplo acima poderíamos escrever: 3 + 3 = 6 ou 2 + 2 + 2 = 6
A figura abaixo mostra o exemplo acima representado pelos círculos vermelhos. Poderíamos somar os círculos um a um. Mas, como agora sabemos multiplicar, basta multiplicar a quantidade de linhas pelas colunas.

Podemos ver pela figura que poderias somar todas os círculos vermelhos, mas basta multiplicar a quantidade de linhas por colunas que teremos o resultado sem precisar contar uma por uma.
Exemplo: 2 x 3 = 6 (leia-se: 2 vezes 3 igual a 6)
No exemplo acima, o número 2 será somado 3 vezes. Veja:
Exemplo: 2 x 3 = 2 + 2 + 2 = 6
Você pode estar pensando: “Contar a quantidade de bolas círculos é mais rápido!”. Bom, neste caso, sim. Agora imagine se tivéssemos 1000 círculos vermelhos.
Propriedades da multiplicação
A seguir apresentaremos algumas das propriedades da multiplicação. É importante prestar bastante atenção, pois algumas das propriedades são importantes para não errar o cálculo.
Comutatividade
A ordem dos fatores não altera o valor do produto.
Exemplos: 3 x 5 = 15 ou 5 x 3 = 15
Independente da forma que se faz a multiplicação dos fatores, o resultado é o mesmo.
Associatividade
Quando multiplicamos três fatores não importa se eles foram agrupados ou não, o resultado é o mesmo.
Exemplos: (3 x 5) x 2 = 30 ou 3 x (5 x 2) = 30
No exemplo acima, os parênteses são agrupamentos dos fatores. Percebemos que o resultado é o mesmo. Não importa a ordem como são multiplicados.
Distributividade
Quando multiplicamos um valor por uma soma, o resultado é a soma do produto desse valor com as parcelas da soma.
Exemplo: 3 x (2 + 3) = (3 x 2) + (3 x 3) = 6 + 9 = 15
Nesse caso, não deve ser resolvido o que está nos parênteses primeiro. Na multiplicação dizemos que o número que está multiplicando o que está nos parênteses, está em evidência.
Assim, pegamos o que está em evidência e multiplicamos por cada valor dentro dos parênteses e depois disso utilizamos o sinal de dentro dos parênteses para realizar a operação com os produtos dessa multiplicação, que nesse caso é uma soma. Isso é o que se chama de distributividade.
Veja na imagem abaixo como fazer, siga a indicação das setas vermelhas:
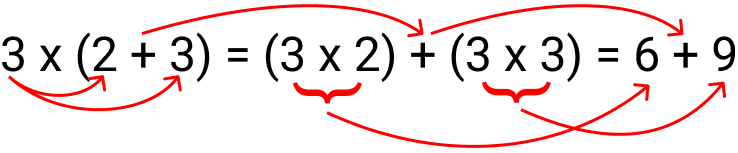
O que fizemos foi pegar o 3 e multiplicar por cada fator de dentro dos parênteses e depois somar, pois, temos uma soma dentro dos parênteses. Poderia ser uma subtração.
Elemento neutro
Na multiplicação o número 1 (um) é o elemento neutro, ou seja, qualquer valor multiplicado por 1 (um) é o próprio valor.
Exemplo: 2 x 1 = 2
Fechamento
O produto de dois ou mais números reais tem como resultado um número real. Isto é, ao multiplicarmos um número do conjunto dos números reais por outro número real, teremos como resultado também um número real.
Anulação
O número 0 (zero) anula qualquer produto.
Exemplos: 2 x 3 x 6 x 0 = 0 ou 10 x 0 = 0
Ordem de multiplicação dos fatores
A ordem que deve ser multiplicado os fatores é da esquerda para a direita para números inteiros, ou seja, número sem casas decimais.
Quando houver números decimais, ou seja, números com vírgula, deve -se começar a multiplicar da direita para a esquerda (quando resolver manualmente). Por fim, contamos a quantidade de casas decimais após a vírgula para colocar corretamente a vírgula no resultado.
Exemplo: 5 x 3,125 = 15,625
Multiplicamos o 5 por todos os números da direita para a esquerda e depois contamos a quantidade de casas após a vírgula e colocamos no resultado final.
Essa mesma ideia serve para resolver manualmente uma multiplicação por números muito grandes.
Exemplo: 5 x 1200 = 6000
Começamos multiplicando o 5 da direta para a esquerda. Assim:
- 5 x 0 = 0;
- 5 x 0 = 0;
- 5 x 2 = 10 (colocar o 0 (zero) e eleva o 1);
- 5 x 1 + 1 = 6.
Temos como resultado 6000. Ficou confuso? Veja a imagem abaixo:

Como multiplicar números com casas decimais manualmente?
Esse é um passo importante. Nem sempre vamos ter uma calculadora por perto e devemos fazer tudo na mão. Veja na imagem abaixo como fazer:

No exemplo, 5 indica quantas vezes vamos somar 3,125. Ou seja, 5 x 3,125 = 3,125 + 3,125 + 3,125 + 3,125 + 3,125 = 15,625.
Assim, para multiplicar manualmente colocamos 3,125 e o número 5 abaixo do último número da direita para a esquerda que nesse caso é o 5. O x indica que estamos fazendo uma multiplicação.
As setas vermelhas indica como devemos seguir multiplicando, da direita para a esquerda. Os números acima de 2 e 1 é o mesmo processo que explicamos na adição.
Quando multiplicamos 5 por 5, resulta em 25, não podemos colocar o valor inteiro. Então, colocamos o valor relativo à unidade (5) e elevamos a dezena (2).
Quando multiplicamos o próximo número, devemos somar esse valor elevado. Por exemplo, quando multiplicamos 5 por 2 temos como resultado o número 10, mas nesse caso foi adicionado o número 2, resultado da operação anterior.
Produtório
Outra forma de representar a multiplicação é o produtório (Π), letra Pi no alfabeto grego. Ele é usado para simplificar.
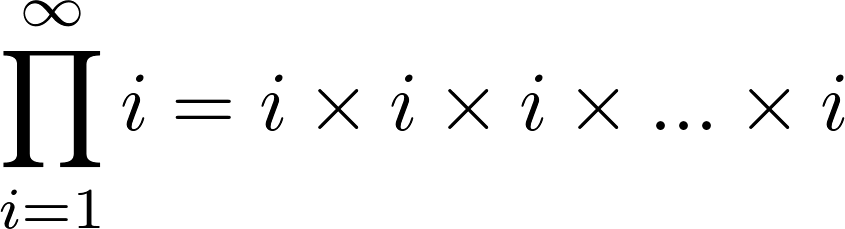
Não conseguiríamos escrever, por exemplo, uma multiplicação infinita de um número. Então, usamos o produtório para mostrar isso.
Na imagem acima temos a variável i sendo multiplicada infinitas vezes, com os limites inferior (i = 1) e superior (símbolo infinito (∞)). Isso mostra que vamos multiplicar a variável i de 1 até o infinito.
Claro que é impossível fazer uma multiplicação assim, mas entenda isso como apenas um exemplo para mostrar como funciona o produtório, que o aluno dever encontrar por aí.
Quando encontrar e surgir uma dúvida, lembra que você aprendeu no Matemática Básica.
Exercícios propostos de multiplição
Responda os exercícios para fixar o que aprendemos até aqui.
Veja também…


