MMC significa mínimo múltiplo comum. O MMC é uma operação para encontrar o menor número positivo, excluindo o zero, que é múltiplo comum entre todos os números dados.
O MMC pode ser usado, por exemplo, para encontrar um denominador comum quando fazemos operações com frações para que o denominador seja comum durante todo o processo.
Os múltiplos de um número podem ser encontrados multiplicando este número pelos números naturais.
Exemplo: 0, 8, 16, 24,32, 40, 48, 56, 64, 72, 80, … são múltiplos de 8, 8 foi multiplicado pelos números naturais 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
O conjunto dos múltiplos de um número é infinito. Perceba que os múltiplos do número 8 foi somando-se de 8 em 8.
Se quisermos saber se um número qualquer é múltiplo de outro, temos que fazer a divisão entre eles. Se obtivermos uma divisão exata, isto é, com resto zero, assim podemos dizer que tal número é múltiplo do outro.
Exemplo:
No exemplo anterior mostramos os múltiplos de 8, então se quisermos saber se 48 é múltiplo de 8 basta dividir 48 por 8: 48 / 8 = 6. Então 48 é múltiplo de 8 pois ele é divisível por 8 com resto zero.
Como calcular o MMC de dois ou mais números?
Para calcular o MMC entre os números dados devemos fazer o seguinte: decompor em fatores primos ou fazer uma decomposição simultânea.
Decomposição em fatores primos
Encontrar o MMC pela decomposição em fatores primos deve obedecer as seguintes regras:
- Decompor os números dados em fatores primos;
- Colocar os fatores primos comuns ou não comuns com seus expoentes maiores;
- Fazer o produto desses fatores primos.
Observação: os números primos são números que são divisíveis somente por ele e por 1 (um).
Exemplo:
Calcular o mínimo múltiplo comum para os números 4, 6 e 12.
- 4 = 2², 2 é um número primo;
- 6 = 2 x 3, três também é primo;
- 12 = 2² x 3.
Agora pegamos os fatores primos comuns e não comuns com os maiores expoentes. Nesse exemplo temos 2 e 3 apenas. Pegamos o 2² e 3, aqui 3 está elevado ao expoente 1.
Assim, o MMC de 4, 6 e 12 é o produto entre 2² x 3 = 4 x 3.
Logo: MMC(4; 6; 12) = 12.
Veja outro exemplo para clarear.
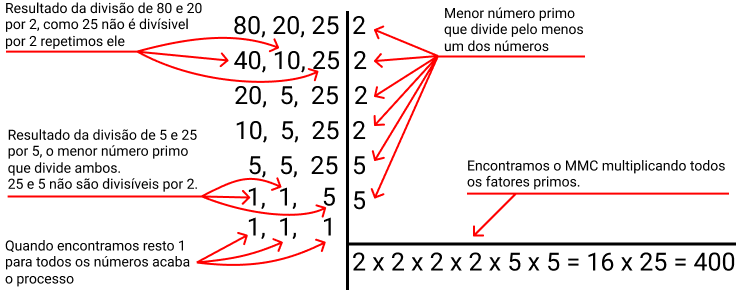
Calcular o MMC de 80, 20, 25:
- 80 = 2 x 2 x 2 x 2 x 5 = 24 x 5;
- 20 = 2 x 2 x 5 = 2² x 5;
- 25 = 5 x 5 = 5².
Dividimos 80 pelo menor número primo que neste caso foi o 2, continuamos dividindo o resultado da divisão por 2, e por último por 5 que era o menor número primos que poderíamos continuar dividindo.
Agora peguemos os fatores primos com os maiores expoentes: 24 e 5². Fazemos o produto entre eles: 24 x 5² = 16 x 25 = 400.
Daí, o MMC(80; 20; 25) = 400.
- Veja exercícios de MMC.
Decomposição simultânea
A decomposição simultânea ou fatoração simultânea consiste em dividir sucessivamente os números dados pelo menor fator primo, caso o número não seja divisível por aquele fator primo ele deve ser repetido.
O MMC é obtido pela multiplicação dos fatores primos usados durante a decomposição. Veja um exemplo para você entender melhor.
Veja como encontrar o menor múltiplo comum entre três números. Se tivermos três números 4, 6 e 8. Qual o MMC desses números através da decomposição simultânea?
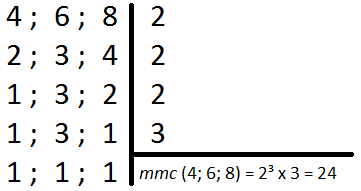
Dividimos 4, 6 e 8 pelo menor número primo que fosse divisível por pelo menor um deles, o número 2. Depois verificamos se ainda tem números que podem ser dividido por 2, 2 e 4 são divisíveis por 2, e conservamos o 3.
No terceiro passo, ainda é possível dividir por 2, mantemos 1 e 3. No quarto passo, só é possível dividir por 3, conservando o resto dos outros números. Quando os restos forem 1, acaba o processo.
O MMC é a multiplicação dos números que dividimos. Utilizamos o 2 três vezes, e o 3 uma vez no processo. Assim temos: 2 x 2 x 2 ou 2³ e 3¹. Logo, 2³ x 3¹ = 24.
Portanto, MMC(4; 6; 8) = 24
Vamos calcular o MMC para o exemplo que usamos fatores primos, agora usando a decomposição simultânea.
Exemplo: Calcular o MMC para 80, 20 e 25.
- Veja exercícios de MMC.
O MMC é usado para somar e subtrair frações, veja nossos artigos sobre soma e subtração de frações para melhor entender.
Propriedades do MMC
- O MMC de dois números primos entre si, é o produto deles;
- O MMC de dois números em que o maior é divisível pelo menor, é o maior deles;
- Multiplicando ou dividindo dois números por outro número diferente de zero, o MMC aparece multiplicado ou dividido por esse outro;
- Dividindo-se o mínimo múltiplo comum de dois números pelo máximo divisor comum entre eles, o quociente obtido é igual ao produto de dois números primos entre si;
- Multiplicando-se o mínimo múltiplo comum de dois números pelo máximo divisor comum entre eles, o resultado obtido é o produto desses números.
A decomposição simultânea tende a ser mais fácil, o aluno pode praticar encontrando o MMC para ouros números para fixar o aprendizado. Responda os execícios abaixo para fixar o que aprendemos.
Exercícios
Acesse os exercícios no link a seguir:
Leia também


