MDC significa máximo divisor comum. O máximo divisor comum entre dois ou mais números naturais é o maior de seus divisores. Dois números naturais sempre têm divisores em comum.
Os divisores de um número natural podem ser encontrados dividindo este número pelos números naturais maiores que zero. Quando a divisão for exata, ou seja, com resto zero, então tal número é divisor do número dado.
Exemplo:
Considere o número 30.
O número 30 é divisível por 30, 15, 10, 6, 5, 3, 2 e 1. Assim, chamamos estes números como os divisores do número 30.
Como calcular o MDC de dois ou mais números?
Para calcular o MDC devemos fazer uma das seguintes operações: decomposição em fatores primos ou decomposição simultânea.
Decomposição em fatores primos
Para encontrar o MDC pela decomposição em fatores primos devemos seguir as seguintes regras:
- Decompor os números dados em fatores primos;
- Pegar os fatores primos comuns com seus expoentes menores;
- Fazer o produto desses fatores.
Exemplo:
Vamos encontrar o máximo divisor comum para os números 16 e 24.
- 16 = 2 x 2 x 2 x 2 = 24
- 24 = 2 x 2 x 2 x 3 = 2³ x 3
Os fatores primos comuns aos dois números dados 24 e 2³. Desses dois temos 2³ com o menor expoente. Logo, 2³ = 8.
Portanto, o MDC(16; 24) = 8, que é o maior número natural que divide ambos os números dados.
Vamos ver mais um exemplo?
Considere os números 30, 50 e 20, o MDC deles é?
- 30 = 2 x 3 x 5
- 50 = 2 x 5 x 5 = 2 x 5²
- 20 = 2 x 2 x 5 = 2² x 5
Os únicos fatores que dividem ambos ao mesmo tempo, são 2 e 5, veja acima na multiplicação dos números primos. Dessa forma pegamos os fatores com menores expoente e fazemos a multiplicação.
Logo, 2 x 5 = 10
Portanto, o MDC(30; 50; 20) = 10
Curiosidade: dois números são primos entre si quando o maior divisor comum (MDC) entre eles é 1.
Exemplo: Sejam 13 e 5, o único número que divide ambos ao mesmo tempo é o número 1.
- Veja os exercícios de MDC.
Decomposição simultânea
A decomposição simultânea ou fatoração simultânea consiste em dividir varias vezes os números dados pelo menor fator primo, se o número não for divisível pelo menor fator, ele deve ser repetido.
O MDC é obtido pela multiplicação dos fatores primos comuns, ou seja, os fatores que dividem os números dados simultaneamente.
Exemplo:
Encontre o máximo divisor comum dos números 180, 240 e 270.
Pela decomposição simultânea devemos dividir simultaneamente os três números dados começando pelo menor número primo possível até chegar ao resto 1.
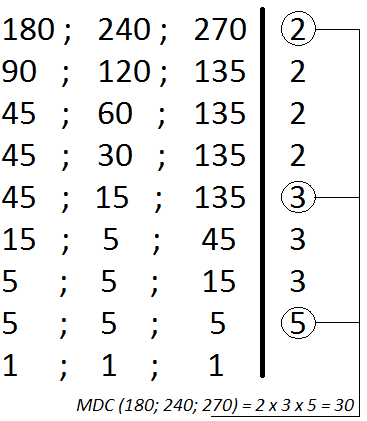
O que fizemos foi dividir os números dados pelo menor primo, o número 2. Dividimos os três números. Depois verificamos se ainda é possível continuar dividindo pelo 2, sim. Os números que não puderem ser divididos devem ser repetidos, como o 135.
Seguimos dividindo pelo 2. Quando não for mais possível dividi-los pelo 2, procuramos o menor número primo possível que possamos dividir pelo menos um deles, neste caso o número primo 3 pode dividir 45, 15 e 135.
Seguimos dividindo pelo 3, quando possível, e conservando aqueles que não podem. Por fim, somente o número 5, que também é primo, pode dividir o número 5, resto das divisões anteriores.
Esse processo acaba quando encontramos resto 1 para todos os números dados. O MDC é a multiplicação dos números primos que puderam dividir todos os números dados ao mesmo tempo.
Portanto, o MDC (180; 240; 270) = 2 x 3 x 5 = 30.
O número 2 dividiu todos os números na primeira vez, o 3 e o 5 também.
Veja mais um exemplo para destruir qualquer dúvida.
Exemplo: calcular o MDC para 20, 50.

- Veja os exercícios de MDC.
Propriedades básicas
- Dados dois ou mais números, se um deles é divisor de todos os outros, então ele é o
MDC dos números dados;
- Exemplo: MDC (3; 6; 12) = 3. O 3 é divisor de 6 e 12, então ele é o máximo divisor comum.
- Dois números consecutivos são sempre primos entre si.
- Exemplo: MDC (25, 26) = 1. O maior número que divide 25 e 26 é 1. Então, ele é o máximo divisor entre 25 e 26.
Exercícios propostos
Veja os exercícios de MDC acessando o link a seguir:
Bons estudos!
Leia também…



