Matriz Transposta: Definição e Propriedades

Uma matriz transposta é uma matriz gerada através da troca ordenada das linhas pelas colunas. A notação para a transposta de uma matriz A é A^t.

Definição

Seja A = [a_ij]_mxn uma matriz qualquer. Chamamos de transposta de A a matriz A^t = [a_ij]_nxm. Ou seja, A^t é obtida a partir de A trocando ordenadamente as linhas pelas colunas.

Perceba que na definição trocamos n por m na matriz transposta.

Onde:

• i é a posição da linha;
• j é a posição da coluna;
• a_ij um elemento de uma posição qualquer na matriz;
• m é o número de linhas na matriz;
• n é o número de colunas na matriz;
• A^t a transposta de A.

Exemplo:

Considere a matriz A, abaixo, então A^t é:

A matriz A é uma matriz de ordem 3×2, ou seja, 3 linhas e 2 colunas. Dessa forma, a matriz A^t terá ordem 2×3, 2 linhas e 3 colunas, pois trocamos as linhas pelas colunas.

Propriedades

Seja A e B matrizes, e a um número real qualquer, então:

• (A + B)^t = A^t + B^t: A transposta da soma de duas matrizes A e B é igual à soma da transposta de A com a transposta de B;
• (a . A)^t = a . A^t: A transposta da multiplicação de um número real a pela matriz A é igual à multiplicação de a pela transposta de A;
• (A^t)^t = A: A transposta da transposta de A é a própria matriz A;
• (A . B)^t = B^t . A^t: A transposta multiplicação da matriz A pela matriz B é igual ao produto da transposta de B pela transposta de A;
• det(A) = det(A^t): O determinante de A é o mesmo determinante da sua transposta A^t.

Matriz Simétrica

Chamamos de matriz simétrica uma matriz quadrada — em que o número de linhas é igual ao número de colunas —, em que vale a igualdade: a_ij = a_ji.

A transposta de uma matriz simétrica A é a própria matriz A, então A = A^t.

Exemplo:

Considere a matriz A a seguir:

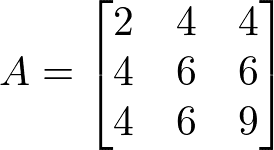
Então a transposta de A é A^t:

Veja que independente de trocarmos as linhas pelas colunas de A, a sua transposta A^t é igual à matriz original A.

Matriz Oposta

Chamamos de matriz oposta de A, a matriz -A. Para obter uma matriz oposta a outra basta trocar os sinais dos elementos de A, sem trocar os elementos de posição.

Exemplo:

Considere a matriz A a seguir:

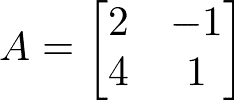
Então a oposta de A é -A, logo:

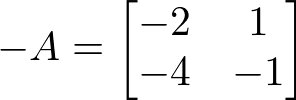
Na matriz oposta apenas trocamos o sinal dos elementos sem trocar a posição dos elementos. Matriz oposta não é a mesma coisa que matriz transposta. Na transposta, nós transportamos os elementos de posição, na matriz oposta apenas mudamos o sinal dos elementos.

Matriz Antissimétrica

Chamamos uma matriz quadrada A de antissimétrica, se A for igual à oposta da transposta de A. Então, temos que: A = -A^t. Então, é equivalente dizer que a_ij = -a_ji.

Os elementos da diagonal principal de uma matriz antissimétrica devem ser, obrigatoriamente, nulos e os elementos que não pertencem à diagonal principal possuem sinais contrários.

Considere a matriz A a seguir:

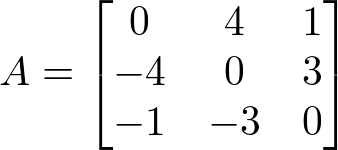
Então a transposta de A é A^t, temos:

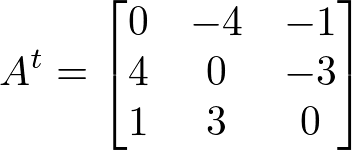
Por fim, a oposta da transposta de A é -A^t:

Logo, A = -A^t

Lembrando que matriz oposta é só trocar os sinais dos elementos da matriz original.

Exercícios

Responda os exercícios propostos:

Resolva os exercícios

Leia também…

• Matrizes
• Matriz Identidade
• Matrizes e Determinantes
• Matriz Inversa
• Tabuada