Responda os exercícios a seguir sobre expressões algébricas para entender como simplificar expressões complexas.
1) Simplifique a expressão algébrica: x³ + 4y + 7x² + 3x³
Ver resposta
Simplificamos adição e subtração em expressões algébricas, realizando as operações nos coeficientes e mantendo a parte literal.
Veja:
x³ + 4y + 7x² + 3x³ ⇒
(1 + 3)x³ + 4y + 7x² ⇒
4x³ + 7x² + 4y
2) Simplifique a expressão: 3x² . 4xy . x² . 5xy . 4x³
Ver resposta
Na multiplicação de monômios, realizamos a multiplicação dos coeficientes e depois das variáveis.
Veja como:
3x² . 4xy . x² . 5xy . 4x³ ⇒
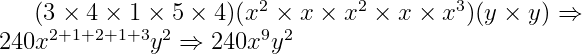
3) Simplifique a expressão: 10x² ÷ 2x
Ver resposta
Realizamos a simplificação desta expressão, dividindo os coeficientes, mantendo as variáveis e subtraindo as respectivas potências.
Veja:
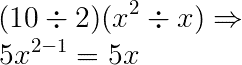
4) Simplifique a expressão: 3x² – 7x² + 4x³ – 5x²
Ver resposta
Simplificamos uma subtração subtraindo os coeficientes e mantendo as variáveis. Fazemos a mesma coisa na adição.
Veja:
3x² – 7x² + 4x³ – 5x² ⇒
(3 – 7 – 5)x² + 4x³ ⇒
-9x² + 4x³ ⇒
4x³ – 9x²
5) Simplifique a seguinte expressão: 4x³ + x³ – 2x² + 5x² – 4y + 8y
Ver resposta
Vamos simplificar realizando as operações sobre os coeficientes e mantendo as variáveis.
Veja:
4x³ + x³ – 2x² + 5x² – 4y + 8y ⇒
(4 + 1)x³ + (- 2 + 5)x² + (- 4 + 8)y ⇒
5x³ + 3x² + 4y
Com esses exercícios você aprendeu a simplificar expressões algébricas. Resolva também os exercícios de expressões numéricas:

