A circunferência é uma figura geométrica plana com forma circular, formada por um conjunto de pontos a uma certa distância de um centro qualquer.
A distância do centro é determinada pelo tamanho do raio (r).
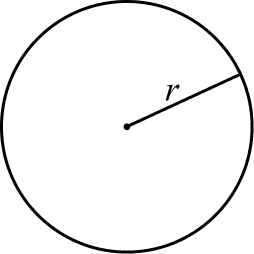
Definição
Seja um ponto C, chamado de centro, e uma medida não nula r, chamada de raio, definimos uma circunferência ao lugar geométrico dos pontos do plano a uma distância r do ponto C.

Corda, Raio e Diâmetro
A corda de uma circunferência é um segmento de reta ligando dois pontos da extremidade. A corda quando passa pelo centro recebe o nome de diâmetro.
O raio é um segmento de reta que conecta o centro a um ponto qualquer da sua extremidade.
O diâmetro é igual a duas vezes a medida do raio, ou seja, é um segmento de reta que conecta um ponto a outro ponto da extremidade, passando pelo centro.
O diâmetro divide a circunferência em duas metades iguais. Então, a medida do diâmetro é 2 . r.

Equação Reduzida
Considere uma circunferência com centro C(a; b) e raio r. Seja um ponto P(x; y) que pertence à circunferência, então temos:
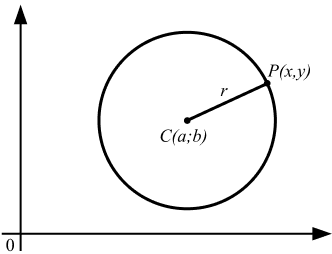
P ∈ a circunferência ⇔ dPC = r ⇔
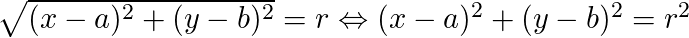
Assim, a equação r² = (x – a)² + (y – b)² é a equação reduzida da circunferência. Se a circunferência estiver com centro na origem C(0; 0), a equação reduzida ficará assim: r² = x² + y².
Equação Geral
Se desenvolvermos a equação reduzida r² = (x – a)² + (y – b)², teremos:
- x² – 2ax + a² + y² – 2by + b² = r² ⇔ x² + y² –2ax– 2by + a² + b² – r² = 0
Se igualarmos -2a = m; -2b = n e a² + b² = p, temos como resultado a expressão:
- x² + y² + m . x + n . y + p = 0
Que é chamada de equação geral da circunferência.
Área
A área é calculada fazendo o produto da medida do raio pela constante π. Para isso, temos a seguinte fórmula:
A = πr²
Onde:
- A: é a área;
- r: é o raio;
- π: é o número pi (3,14).
Leia mais sobre áreas de figuras planas.
Perímetro
O perímetro é a medida da borda da figura. Que é calculado pelo produto entre o raio e duas vezes a constante π. Então, para calcular o perímetro temos a seguinte fórmula:
P = 2 . π . r
Onde:
- P: é o perímetro;
- r: é o raio;
- π: é o número pi (3,14).
Leia mais sobre perímetros de figuras planas.
Comprimento
O comprimento é determinado pelo tamanho do raio, que é igual a calcular a medida do perímetro.
Assim, para calcular o comprimento usamos a seguinte fórmula:
C = 2 . π . r
Onde:
- C: é o comprimento;
- r: é o raio;
- π: é o número pi (3,14).
Circunferência e Círculo
Circunferência e círculo possuem uma diferença sutil, porém não são a mesma coisa. A circunferência é denominada a borda curva da figura e o círculo é a parte interna limitada pela linha curva.

Ambas as figuras planas são bem parecidas, inclusive as fórmulas para calcular a área e o perímetro são iguais.
Leia sobre o círculo:
Exercícios
Acesse os exercícios no link a seguir:


