A área do círculo é a medida equivalente à superfície dessa figura plana, calculada pelo produto entre a medida do raio (r) ao quadrado e a constante π (3,14).

Como é definido o Círculo?
O círculo, também chamado de disco, na matemática, é um conjunto de pontos na parte interna da circunferência. Dessa forma, a distância dos pontos do círculo para o centro é menor ou igual ao tamanho do raio r.
Como um Círculo é formado?
O círculo é formado através de um polígono que vai aumentando seu número de lados. Assim, quanto mais lados um polígono tem, mais ele se aproxima de uma forma circular. Veja na figura abaixo esse processo:
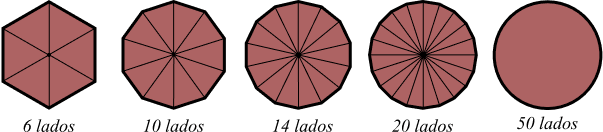
Pela imagem podemos ver que o polígono possui vários triângulos e o cálculo da área desse polígono seria igual à soma das áreas de todos os triângulos.
No entanto, quando aumentamos a quantidade de lados, o polígono começa a tomar uma forma circular. Dessa forma, a área desse polígono é equivalente a calcular a área de um círculo.
O que é uma Circunferência?
A circunferência é formada por um conjunto de pontos que distam do centro C por uma medida r chamada de raio. Então, a linha que forma a circunferência são pontos com a mesma distância do centro.

Na imagem temos P representando um ponto que dista do centro C pela medida do raio r. Entenda que a linha que forma a circunferência seja formada por vários pontos P na mesma distância r do centro C.
Leia mais sobre a circunferência.
Área do Círculo
A área do círculo é calculada através do produto entre a constante π e a medida do raio ao quadrado (r²). Assim, temos a seguinte fórmula:
- A = π . r²
Onde:
- A: é a área;
- π: é o número pi (3,14)
- r: é a medida do raio.
A área do círculo é igual a calcular a área da circunferência. Lembrando que a medida da área do círculo e da circunferência é uma medida aproximada.
O raio é a medida que vai do centro até um ponto da extremidade do círculo. O diâmetro é a medida equivalente ao dobro da medida do raio, passando pelo centro do círculo e dividindo-o em duas partes. A medida do diâmetro é 2 . π.
Perímetro do Círculo
O perímetro do círculo é a medida equivalente à linha curva que forma a borda circular. O perímetro é calculado através do produto entre o raio e o dobro da constante π. Assim, temos a seguinte fórmula:
P = 2 . π . r
Onde:
- P: é o perímetro;
- π: é o número pi (3,14);
- r: é o raio.
O perímetro do círculo é igual calcular o perímetro da circunferência. Lembrando que o perímetro é também uma medida aproximada.
Diferença entre Círculo e Circunferência
Existem uma diferença sutil que passa despercebida entre o círculo e a circunferência. A circunferência é a linha do círculo e o círculo é a parte interna da circunferência.

Pelo fato da área do círculo e da circunferência ser calculada pela mesma fórmula, contribui para essa confusão. Mas o círculo é a parte interna e é limitada pela circunferência.
Exercícios
Acesse os exercícios no link a seguir:


