Área do Cilindro: Fórmula e Exercício Resolvido

A área do cilindro é a soma da área lateral com o dobro da área da base dessa figura da geometria espacial.

O cilindro é uma figura tridimensional com duas bases circulares, uma superior e a outra inferior. A altura é que define o tamanho da figura.

As bases do cilindro são paralelas entre si. Além disso, elas possuem o mesmo diâmetro.

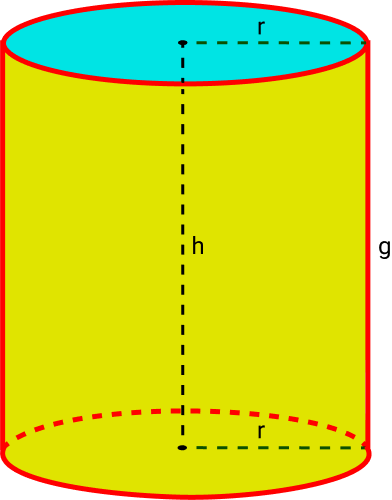
Como Calcular a Área do Cilindro?

Para calcular a área do cilindro precisamos calcular primeiro as áreas da base e da superfície cônica lateral.

Planificação do Cilindro

Para entendermos como é calculada a área do cilindro precisamos entender como é calculada a área lateral do cilindro.

Esse cálculo pode ser entendido se abrirmos o cilindro e realizar algumas observações. Esse processo é chamado de planificação.

Se abrirmos a lateral do cilindro temos um retângulo. O lado maior corresponde ao perímetro da base, ou seja, a medida da borda do círculo. O perímetro da circunferência é igual a 2 . π . r que é a medida maior da lateral planificada. O lado menor é a medida equivalente à altura do cilindro. Como podemos ver na figura a seguir:

Área Lateral

A área lateral do cilindro é calculada através da fórmula da área do retângulo: A = b . h. A base (b), neste caso, é 2 . π . r. A altura é h.

Substituindo na fórmula da área do retângulo, temos a seguinte fórmula para a área lateral do cilindro:

• A_l = 2 . π . r . h

Onde:

• A_l: é a área lateral;
• π: é o número pi (3,14);
• r: é o raio da base;
• h: é a altura do cilindro.

Área da Base

A área da base é equivalente a calcular a área de uma circunferência. Assim, temos a seguinte fórmula:

A_b = π . r²

Onde:

• A_b: é a área da base;
• π: é o número pi (3,14)
• r: é o raio da base;

Área Total

A área total do cilindro é a soma da área lateral com a área da base. Como o cilindro possui duas bases com a mesma medida, temos que considerar o dobro da área da base. Assim, a fórmula para a área total do cilindro é:

A_t = 2 . A_b + A_l = 2 . (π . r²) + 2 . π . r . h = 2 . π . r . (h + r)

Onde:

• A_t: é a área total;
• A_b: é a área da base;
• A_l: é a área lateral;
• π: é o número pi (3,14);
• r: é o raio da base;
• h: é a altura do cilindro.

Leia mais sobre o cilindro.

Veja também como calcular o volume do cilindro.

Exercício Resolvido

1. Seja um cilindro de 20 cm de altura e raio da base de 5 cm. Calcule a área total desse cilindro.

Dados do problema:

Altura: 20 cm

Raio da base: 5 cm

Área lateral:

• A_l = 2 . π . r . h ⇒
• A_l = 2 . π . 5 . 20 ⇒
• A_l = 200π cm²

Área da base:

• A_b = π . r² ⇒
• A_b = π . 5² ⇒
• A_b = 25π cm²

Área total:

• A_t = 2 . A_b + A_l ⇒
• A_t = 2 . 25π + 200π ⇒
• A_t = 50π + 200π ⇒
• A_t = (50 + 200)π ⇒
• A_t = 250π cm²

Lembrete: a unidade de medida da área é o metro quadrado (m²).

Exercícios Propostos

Acesse os exercícios propostos no link a seguir:

• Exercícios sobre a área do cilindro