O volume da esfera corresponde a medida do espaço interno da figura. Assim, o volume é calculado utilizando a medida do raio, a medida equivalente a um ponto na superfície da esfera ao centro.

O volume é uma medida de capacidade. Assim sendo, esse conceito só é utilizado em figuras da geometria espacial e corresponde a calcular a medida utilizando três variáveis (x, y e z) sendo as coordenadas para figuras tridimensionais.
A unidade de medida para o volume é o metro cúbico (m³).
Como Calcular o Volume da Esfera?
No cálculo do volume da esfera utilizamos a seguinte fórmula:
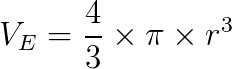
Onde:
- VE: é o volume da esfera;
- π: é o número pi (3,14);
- r: é a medida do raio da esfera.
Partes da Esfera
A esfera é divida em quatro partes que podem ser estudadas: cunha esférica, setor esférico, segmento esférico de uma base e o segmento esférico de duas bases.
Cunha Esférica: a cunha esférica é uma região tridimensional formada por dois semicírculos e o eixo de rotação da esfera. Podemos comparar, por exemplo, com o gomo de uma laranja;
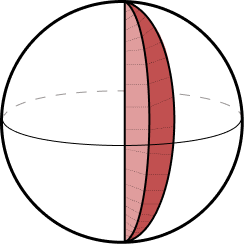
Setor esférico: o setor esférico é uma região compreendia entre uma região que foi cortada por dois planos paralelos entre si e perpendiculares ao eixo da esfera;
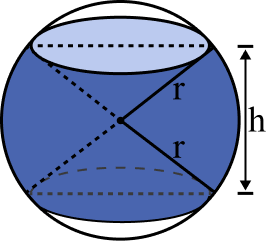
Segmento esférico de uma base: é um segmento de uma esfera que foi cortada por um plano perpendicular ao eixo da esfera;
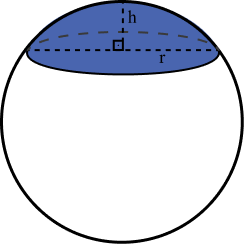
Segmento esférico de duas bases: é um segmento de uma esfera que foi cortada por dois planos paralelos entre si e perpendicular ao eixo de rotação da esfera.
Volume da Cunha Esférica
Calculamos o volume da cunha esférica utilizando a seguinte fórmula, a saber:
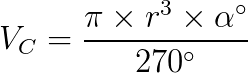
Onde:
- VC: é o volume da cunha;
- π: é o número pi (3,14);
- r: é a medida do raio da esfera;
- α: é o ângulo da cunha esférica.
Volume do Setor Esférico
O volume do setor esférico é calculado pela seguinte fórmula:
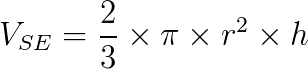
Onde:
- VSE: é o volume do setor;
- π: é o número pi (3,14);
- r: é a medida do raio da esfera;
- h: é a medida da altura do setor.
Volume do Segmento Esférico de uma Base
Para calcular o volume do segmento esférico de uma base usamos a seguinte fórmula:
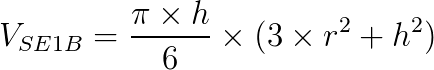
Onde:
- VSE1B: é o volume do segmento;
- π: é o número pi (3,14);
- r: é a medida do raio da esfera;
- h: é a altura do segmento.
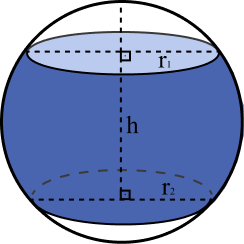
Volume do Segmento Esférico de Duas Bases
Usamos a seguinte fórmula no cálculo do volume do segmento esférico de duas bases:
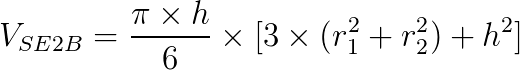
Onde:
- VSE2B: é o volume do segmento de duas bases;
- π: é o número pi (3,14);
- r1: é a medida do raio da base 1;
- r2: é a medida do raio da base 2;
- h: é a medida da altura do segmento.
Leia mais sobre o assunto:



