O triângulo retângulo é um tipo especial de triângulo que recebe esse nome porque possui um ângulo reto, ou seja, um ângulo que mede 90°. Os outros dois ângulos internos são inferiores a 90°, chamados ângulos agudos.
Considere o triângulo ABC a seguir:
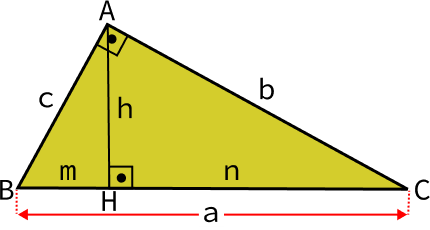
Onde:
- b e c são os catetos oposto e adjacente, respectivamente;
- a é a hipotenusa;
- h é a medida da altura;
- m é a projeção ortogonal do cateto AB sobre a hipotenusa;
- n é projeção ortogonal do cateto AC sobre a hipotenusa.
A altura do triângulo, dependendo de qual seja a sua base, ela pode ser igual a um dos lados do triângulo.

Área do Triângulo Retângulo
A área é calculada da seguinte forma:

A fórmula é idêntica à fórmula geral para o cálculo da área do triângulo, porém devemos ficar atento, pois dependendo de qual seja a base do triângulo, o valor referente a altura pode ser igual a um dos lados.
Medida da Mediana relativa a Hipotenusa
Em qualquer triângulo retângulo, a medida em relação à mediana, ou seja, o ponto médio entre os vértices da hipotenusa, mede a metade da hipotenusa.

Podemos demonstrar que a mediana é realmente a metade da hipotenusa da seguinte forma: se pegarmos o triângulo retângulo acima e duplicarmos ele formando dois, unirmos esses triângulos pela hipotenusa teremos um retângulo onde a mediana dos dois se intercepta na metade do retângulo.
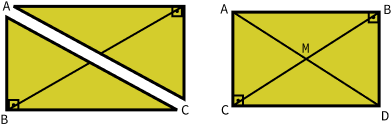
Logo M é o ponto médio da hipotenusa para o triângulo ABC.
Assim, como AD = BC e AM = AD/2, então AM = BC/2
Também podemos verificar que essa propriedade é verdadeira através da circunferência circunscrita ao triângulo retângulo.
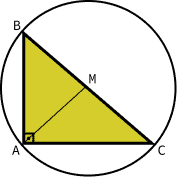
Dessa forma, fazendo com que os vértices do triângulo fique sobre o círculo da circunferência e o ângulo inscrito na circunferência é um ângulo reto, o arco
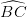
que ele enxerga mede 180°. Assim, o segmento de reta do triângulo retângulo
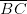
é o diâmetro da circunferência, e M, o ponto médio, é o centro da circunferência.
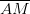
é a mediana.
Portanto, como ela é igual ao raio da circunferência, temos que AM = BC/2
Teorema de Pitágoras para o triângulo retângulo
O Teorema de Pitágoras nos diz que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. Em muitos problemas esse teorema pode ser empregado na resolução do problema, por exemplo, se dois lados tem valores conhecidos podemos achar o valor do terceiro. O mesmo também vale para a altura do triângulo retângulo.
Teorema de Pitágoras: a² = b² + c²
Exercícios
Acesse os exercícios através do link abaixo:


