Chamamos de retas paralelas duas retas distintas que possuem os mesmos coeficientes angulares e coeficientes lineares diferentes. As retas paralelas não se cruzam, portanto não há pontos em comuns entre elas e a distância entre elas são sempre iguais.
Retas paralelas cortadas por uma transversal
Euclides propôs que a condição para que duas retas sejam paralelas é uma reta transversal, não perpendicular, que corta às duas formando ângulos alternados congruentes.
Essa proposição de Euclides pode ser visto na imagem a seguir:
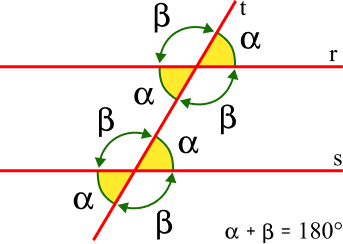
Seja duas retas r e s, paralelas entre si e uma transversal t, não perpendicular a r e s. Temos que os 8 (oito) ângulos formados pela reta transversal com as retas r e s, quatro deles serão agudos (α) e congruentes (mesma medida), os outros quatro serão obtusos (β) e congruentes. Além disso, os ângulos obtusos e agudos serão suplementares (medem 180°).
Os ângulos β (beta) tem medidas iguais, assim como os ângulos α (alfa). E a soma de α + β é 180°, dessa forma eles são suplementares.
Os ângulos formados pelas retas paralelas com a transversal são nomeados como: ângulos correspondentes, alternos e colaterais
Ângulos Correspondentes
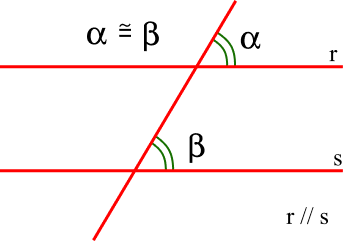
Os ângulos correspondentes são aqueles que possuem as mesmas medidas e ocupam a mesma posição. Na imagem os ângulos α e β, além de ocuparem a mesma posição, são congruentes.
Ângulos Alternos
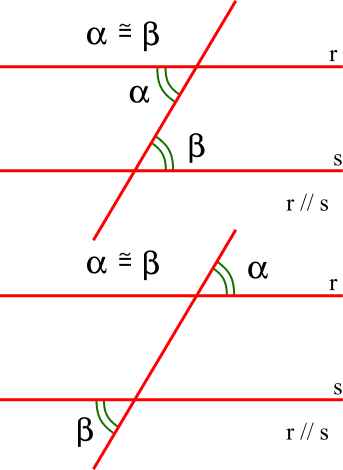
Os ângulos alternos são os ângulos que estão em lados opostos. Os ângulos α e β estão em lados diferentes da reta transversal. Além disso, os ângulos alternos são congruentes. Eles também podem está dentro ou fora das retas r e s.
Ângulos Colaterais
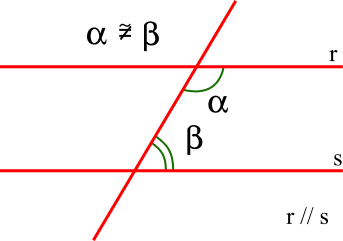
Os ângulos colaterais são aqueles que estão do mesmo lado da reta transversal, mas em posições diferentes. Eles não são congruentes. Porém, são suplementares, ou seja, a soma das suas medidas é igual a 180°.
Teorema de Tales
Seja as retas paralelas a, b e c cortadas pelas retas transversais r e s. Como mostra a figura a seguir:
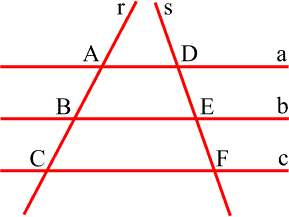
Tales afirma que quando um feixe de retas paralelas são cortadas por duas retas transversais, os segmentos formados nas retas transversais são proporcionais.
Observando a imagem acima, os segmentos AB e DE, BC e EF e AC e DF são segmentos proporcionais. Assim, segundo o Teorema de Tales, a razão entre os segmentos correspondentes nas duas transversais é constante, então:
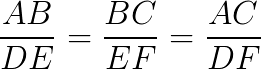
Exercícios Resolvidos sobre retas paralelas
1) Encontre os valores para x e y que
corresponde as medidas dos ângulos na figura:

Resolução:
Ao analisar a imagem percebe-se que x e 60° são ângulos alternos. Em retas paralelas cortadas por uma transversal os ângulos alternos são congruentes. Portanto, x = 60°
O ângulo ao lado de y é correspondente ao ângulo de 60°, dessa forma podemos encontrar a medida de y assim:
Como y e 60° são suplementares, a soma deles mede 180°.
- y = 180° – 60° = 120°
2) Dadas as equações gerais das retas r e s a seguir, verifique se elas são paralelas entre si.
- r: -2x + y + 2 = 0
- s: -2x + y + 4 = 0
Resolução:
A equação de r e s pode ser escrita da seguinte forma:
- r: y = arx + br
- s: y = asx + bs
Duas retas são paralelas entre si se os seus coeficientes angulares são iguais: ar = as
Para responder à questão precisamos encontrar o coeficiente angular de cada reta através da equação de cada reta.
Coeficiente angular da reta r:
- -2x + y + 2 = 0 ⇒
- y = 2x – 2
- mr = 2
Coeficiente angular da reta s:
- -2x + y + 4 = 0 ⇒
- y = 2x – 4
- ms = 2
Assim, como os coeficientes angulares das retas r e s são iguais, temos que as duas retas são paralelas.
Exercícios
Acesse os exercícios no link a seguir:


