A função logarítmica é a função do tipo f(x) = logax, em que a é a base do logaritmo da função, a é positivo e a ≠ 1.
O logaritmo é usado para descobrir o valor do expoente de uma base qualquer. Assim, o logaritmo de um número b com base a, é o expoente x, que é potência da base e resulta em b.

Para entender o logaritmo é necessário estudar e entender potenciação.
Definição
A função logarítmica é uma função f: R*+ → R, definida como f(x) = logax, em que 0 < a ≠ 1.
Domínio da Função Logarítmica
Como podemos ver pela definição acima, o domínio da função logarítmica está contido no conjunto R*+, conjunto dos reais positivos sem o 0 (zero).
O domínio da função logarítmica são os valores que podemos aplicar a variável x.
Lembrando que o logarítmico e a base tem que ser positivos, e a base tem que ser diferente de 1.
Exemplo:
Seja f(x) = log22x + 1, determine o domínio da função.
Resolução:
A resolução dessa questão é bem simples, temos apenas que tomar cuidado com a condição de existência do logaritmo, como podemos ver 0 < a ≠ 1. Então, 2x + 1 > 0 ⇒ 2x > -1 ⇒ x > –1⁄2
Assim, o domínio dessa função é definido assim:
D = {x ∈ R | x > –1⁄2 }
Gráfico
Para entendermos o gráfico, vamos aplicar alguns valores em uma função e esboçar o gráfico para ver o resultado e seu comportamento no plano cartesiano.
Podemos classificar funções logarítmicas em crescente e decrescente conforme o seu gráfico.
Função Crescente
Uma função logarítmica com base a > 1 é estritamente crescente e contínua em R*+. Dessa forma, se aplicarmos valores na função f(x) = log2x temos a seguinte tabela:
| x | f(x) = log2x |
|---|---|
| 1⁄4 | -2 |
| 1⁄2 | -1 |
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
Com esses valores em mãos vamos construir o gráfico.
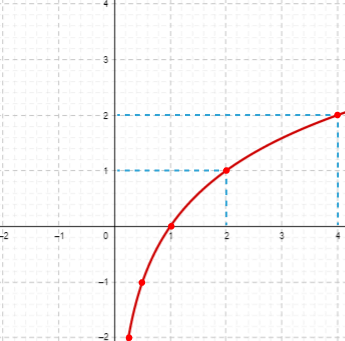
Veja que temos um gráfico crescente e cresce mais lentamente ao longo do tempo, quando os valores de x aumentam.
Função Decrescente
Uma função logarítmica com base 0 < a < 1 é estritamente decrescente e contínua em R*+. Assim, aplicando valores na função f(x) = log1⁄2x, temos a seguinte tabela:
| x | f(x) = log1⁄2x |
|---|---|
| 1⁄4 | 2 |
| 1⁄2 | 1 |
| 1 | 0 |
| 2 | -1 |
| 4 | -2 |
Colocando esses valores no gráfico, temos:
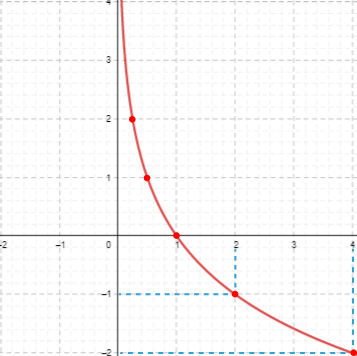
O gráfico é decrescente e quando os valores para x aumentam o gráfico decresce mais lentamente.
Resumindo, podemos afirmar que a função logarítmica é:
- Injetora e Sobrejetora;
- Estritamente crescente, para a > 1;
- Estritamente decrescente, para 0 < a < 1
Sinal do Logaritmo
O sinal do logaritmo pode ser negativo ou positivo, e podemos saber o sinal nas seguintes condições:
- Se a > 1:
- logax > 0 ⇔ x > 1
- logax < 0 ⇔ 0 < x < 1
- Se 0 < a < 1:
- logax > 0 ⇔ 0 < x < 1
- logax < 0 ⇔ x > 1
A função inversa da logarítmica é a função exponencial.
Exercícios
Veja os exercícios no link a seguir:


