Logaritmo: Propriedades e Mudança de Base

Logaritmo é a operação inversa da exponenciação. Isto quer dizer que o logaritmo de um número y qualquer na base b, é um expoente x elevado a base b, de forma que b^x produz como resultado y.

• y = b^x ⇔ x = log_b(y)

Definição

Seja dois números reais positivos a e N , de forma que a ≠ 1, chamamos logaritmo de N na base a, um expoente x, o qual elevado a a, produzimos N como resultado.

• log_a N ⇔ a^x = N

Onde:

• N: é o logaritmando ou antilogaritmo;
• a: é a base;
• x: é o logaritmo.

Exemplo:

• log₆ 36 = 2, pois 6² = 36
• log₁₀ 100 = 2, pois 10² = 100

Condição de Existência

O log_aN existe se, e somente se, as seguintes condições forem verdadeiras:

• N > 0;
• a > 0;
• a ≠ 1.

Logaritmo com Representação Especial

Temos duas representações especiais:

• Logaritmo decimal: log a = log₁₀a, quer dizer que se não explicitamos a base, a base do logaritmo é 10.
• Logaritmo neperiano: ln a = log_ea, em que e = 2,71828182… sendo um número irracional, conhecido também como número de Euler.

Consequência da Definição dos Logaritmos

A partir da definição dos logaritmos, em que a > 0, a ≠ 1, N > 0 e n um número real, podemos afirmar que:

• log_a1 = 0;
• log_aa = 1;
• log_aaⁿ = n;
  • Exemplo: log₂2⁵ = 5, pode cortar o logaritmo e o resultado é o expoente.
• a^log_aN = N;
  • Exemplo: 3^log₃4 = 4, pode cortar o logaritmo e a base da potência.

Propriedades

Seja M > 0, a ≠ 1, a > 0 e N > 0, as seguintes propriedades para os logaritmos são verdadeiras:

• log_a(M . N) = log_aM + log_aN;
• log_a(M/N) = log_aM – log_aN;
• log_a(N^m) = m . log_aN ∀m ∈ R;

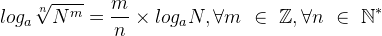
Mudança de Base

Considere log_ab, tal que a > 0, a ≠ 1 e b > 0. Se quisermos trocar a base a para uma base c, em que c > 0 e c ≠ 1, devemos seguir a seguinte propriedade:

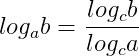
Onde:

• log_ca ≠ 0, isto é, a ≠ 1.

Exemplo:

Escreva log₃4 na base 4:

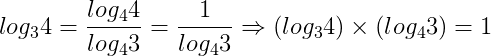
Escreva log₅8 na base 2:

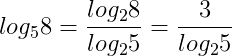
Cologaritmo

Cologaritmo é um tipo especial de logaritmo, podemos expressá-lo da seguinte forma:

• colog_ab = – log_ab

Também podemos dizer que:

• colog_ab = log_a(1/b)

Como resolver um logaritmo?

Resolver logaritmo parece bastante complicado, mas praticando torna-se mais fácil. Vamos demonstrar como encontrar o logaritmo de um número dado.

A definição diz que:

log_a N = x ⇔ a^x = N

Então, vamos aplicar em um exemplo para entendermos o que a definição diz.

Exemplo:

Calcule o log₅125:

A definição nos diz que: log₅ 125 = x ⇔ 5^x = 125. Ou seja, o logaritmo de 125 na base 5 é x, de forma que 5 elevado a x seja igual a 125. Então, temos que encontrar qual número elevamos a 5 que seja igual a 125.

Assim, para encontrar o valor de x, vamos fatorar o número 125.

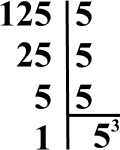
Veja que dividimos 125 pelo seu MMC, ou seja, o menor número que poderíamos dividi-lo. O mesmo para os outros resultados. Como dividimos 3 vezes pelo número 5, então x = 3.

Logo, 5^x = 5³ = 125.

Portanto, log₅ 125 = 3.

Exercícios

Acesse os exercícios no link abaixo:

• Exercícios propostos