Responda os exercícios a seguir que preparamos com operações envolvendo números complexos.
1) Determine a soma dos números complexos: z1 = 3 – 2i e z2 = 5 + 6i
Ver resposta
A adição de dois números complexos é dada por:
z1 + z2 ⇒
(3 – 2i) + (5 + 6i) ⇒
3 + 5 + 6i – 2i ⇒
(3 + 5) + (6 – 2)i ⇒
8 + 4i
2) Calcule a diferença dos seguintes números complexos: z1 = 4 – 3i e z2 = 7 + 2i
Ver resposta
Resolvemos a subtração de dois números complexos assim:
z1 – z2 ⇒
(4 – 3i) – (7 + 2i) ⇒
(4 – 7) + (- 2 – 3)i ⇒
– 3 – 5i
3) Faça o produto sobre os números complexos: z1 = 8 + 2i e z2 = 7 + i
Ver resposta
O produto entre dois complexos é realizado como a seguir:
z1 x z2 ⇒
(8 + 2i)(7 + i) ⇒
8 . 7 + 8 . i + 2i . 7 + 2i . i ⇒
56 + 8i + 14i + 2i² ⇒
56 + 22i + 2(-1) ⇒
56 + 22i – 2 ⇒
56 – 2 + 22i ⇒
54 + 22i
4) Determine o resultado da divisão dos números complexos: z1 = 6 + 2i e z2 = 2 – 3i
Ver resposta
Veja como realizamos a divisão de dois complexos:

5) Se i é a unidade imaginária do conjunto dos números complexos, determine o resultado para os números complexos 2i + i³ – 23 + 5i²
Ver resposta
2i + i³ – 23 + 5i² ⇒
2i + (-i) – 23 + 5(-1) ⇒
2i – i – 23 – 5 ⇒
– 28 + i
6) Resolva a equação do segundo grau 2x² + 2x + 1 = 0
Ver resposta
Os coeficientes da equação do segundo grau são:
a = 2
b = 2
c = 1
Encontrando o valor do discriminante delta (Δ):
Δ = 2² – 4 . 2 . 1 = 4 – 8 = -4
Antes de estudamos sobre os números completos, aprendemos que equação com resultado do discriminante delta igual a número negativo não possui solução no conjunto dos números reais (R).
No entanto, podemos resolver este tipo de equação agora que conhecemos os números complexos.
Então,
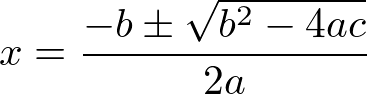
x1 = (- 2 + √(4 . (-1)))/4 = (-2 + 2√-1)/4 = (-2 + 2i)/4
x2 = (- 2 – √(4 . (-1)))/4 = (-2 – 2√-1)/4 = (-2 – 2i)/4
Portanto, os valores de x que são raízes da equação é dado por (-2 + 2i)/4 e (-2 – 2i)/4.
Este são alguns exercícios com números complexos para contribuir no aprendizado.


