O coeficiente angular é o valor que determina a inclinação de uma reta no plano cartesiano. Então, se o coeficiente for positivo a reta é ascendente, caso contrário, a reta é descendente.
Fórmula
No cálculo do coeficiente utilizamos a seguinte fórmula:
m = tg(θ)
Onde:
- m: é um número real qualquer;
- θ: é o ângulo que define a inclinação da reta.
Casos Particulares
- Quando θ = 0°: a tangente é nula;
- Quando 0° < θ < 90°: a tangente é positiva e está no 1º quadrante;
- Quando θ = 90°, ou seja, o ângulo é reto: não temos como calcular o coeficiente angular, pois não existe tangente para o ângulo reto;
- Quando 90° < θ < 180°: a tangente é negativa e está no 2º quadrante.
Cálculo do Coeficiente Angular
O cálculo é feito a partir de dois pontos que correspondem a variação entre os eixos x e y.
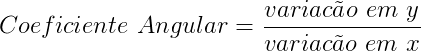
A reta passa pelos pontos A(xa, ya) e B(xb, yb, assim:

Simplificando:

Onde:
- Δy: é a diferença entre os valores das ordenadas dos pontos A e B;
- Δx: é a diferença entre os valores das abcissas dos pontos A e B;

Exemplo:
Seja r uma reta qualquer, e A(-2, 3) e B(4, 1) pontos que a reta r passa. Calcule o coeficiente angular da reta r.
- m = Δy/Δx
- m = (y – y0)/(x – x0)
- m = (3 – 1)/(-2 – 4)
- m = 2/-6
- m = – 1⁄3
Como o coeficiente é negativo temos uma ideia de como é o gráfico, é descendente.
Equação da reta a partir do Coeficiente Angular e um ponto da reta
Seja a reta r com coeficiente angular m. Na reta r, consideremos os pontos P(x0, y0), tal que P ∈ r, e Q(x, y) um ponto qualquer da reta r de forma que r(Q ≠ P). Então:
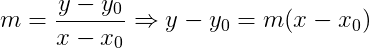
Exemplo:
Seja uma reta r que passa pelos pontos P(2, 3) e o coeficiente m = 2, com x0 = 2 e y0 = 3. Determine a equação da reta r.
Resolução:
- y – y0 = m(x – x0) ⇒
- y – 3 = 2(x – 2) ⇒
- y – 3 = 2x – 4 ⇒
- 2x – y – 1 = 0
Exercícios
Acesse os exercícios no link abaixo:


