O cilindro é uma figura geométrica espacial com formato circular, possuindo o mesmo diâmetro em todo o seu comprimento.
Possui duas bases circulares e paralelas entre si, com o mesmo raio.
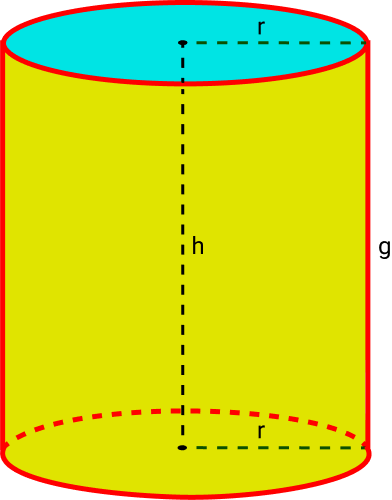
Elementos do Cilindro
O cilindro é composto por alguns componentes essenciais a sua existência, são eles:
- Base: o cilindro possui duas bases opostas, congruentes (mesma medida) e paralela entre si. Uma base é superior e a outra é a base inferior.
- Raio: as bases possuem a forma circular, como toda circunferência ela possui um raio que inicia no centro até a linha da base.
- Geratriz: a geratriz são os segmentos de retas que vai de uma extremidade de uma base a outra, e equivale à altura do cilindro (h = g).
- Diretriz: é o ponto de cada geratriz na base, a diretriz é que indica a direção de cada segmento de reta.
Classificação dos Cilindros
Os cilindros podem ser classificados conforme o seu formato, que pode ser reto ou oblíquo. Dessa forma, se a altura for perpendicular as bases, temos um cilindro reto, caso contrário, temos um cilindro oblíquo.
Reto
Um cilindro é considerado reto quando a geratriz (altura), ou seja, a reta que forma a lateral do cilindro de uma base a outra, for perpendicular as bases.

Oblíquo
Um cilindro é considerado não reto ou oblíquo, quando a geratriz não for perpendicular as bases

Equilátero
Um cilindro é considerado equilátero quando o diâmetro das bases for igual à geratriz (altura), ou seja, quando a altura for igual a 2r.

Cilindro de Revolução
Um cilindro também podem ser um sólido de revolução. Os sólidos de revolução são aqueles que podem ser obtidos através de uma rotação de um plano em torno de um eixo.
No caso do cilindro, ele é obtido pela rotação de um plano retangular.

Como Calcular a Área do Cilindro?
Para calcular a área, precisamos saber calcular a área da base e da lateral do cilindro. A área total é a soma das áreas da base e da lateral.
Área da Base
A área da base é equivalente a calcular a área de uma circunferência. Assim, para calcular a área da base usamos a seguinte fórmula:
Ab = π . r²
Onde:
- Ab: é a área da base;
- π: é o número pi (3,14);
- r: é o raio da base.
Área Lateral
Para calcular a área lateral do cilindro, temos que considerar também a altura e o diâmetro da base. Então, utilizamos a seguinte fórmula:
Al = 2 . π . r . h
Onde:
- Al: é a área lateral;
- π: é o número pi (3,14);
- r: é o raio da base;
- h: é a altura.
Área Total
A área total é a soma das áreas da base e da lateral. Como o cilindro possui duas bases, ao somar as bases temos que considerar o dobro da medida da área da base. Assim, utilizamos a seguinte fórmula:
At = 2 . Ab + Al ou At = 2 . (π . r²) + (2 . π . r . h)
Onde:
- At: é a área total;
- Ab: é a área da base;
- Al: é a área lateral;
- π: é o número pi (3,14);
- r: é o raio da base;
- h: é a altura.
Como Calcular o Volume do Cilindro?
O volume é calculado realizando o produto da medida da área da base pela medida da altura (geratriz). Então, o volume é calculado usando a seguinte fórmula:
V = Ab . h ou V = π . r² . h
Onde:
- V: é o volume;
- Ab: é a área da base;
- h: é a altura;
- π: é o número pi (3,14);
Exercício Resolvido
Um tambor com 110 cm de altura e raio da base medindo 60 cm. Calcule a área da base, da lateral e total do tambor. Calcule também a capacidade desse tambor.
Resolução:
Para resolver o problema precisamos utilizar as fórmulas para cada uma das áreas e do volume.
Área da base
- Ab = π . r² ⇒ Ab = π . (60)² ⇒ Ab = 3600π cm²
Área lateral:
- Al = 2 . π . r . h ⇒ Al = 2 . π . 60 . 110 ⇒ Al = 13200π cm²
Área total: a área total é a soma da área lateral pelo dobro da área da base.
- At = 2 . Ab + Al ⇒ At = 2 . 3600π + 13200π ⇒ At = 20400π cm²
Capacidade ou volume: para calcular a capacidade basta usar a fórmula do volume direto.
- V = π . r² . h ⇒ V = π . (60)² . 110 ⇒ V = π . 3600 . 110 ⇒ V = 396000π cm³
A unidade de medida usada no cálculo da área é o metro quadrado (m²) e no volume é o metro cúbico (m³). Sabemos que cm² e cm³ são submúltiplos do m² e m³, respectivamente.
Exercícios Propostos
Veja os exercícios propostos no link abaxio:


