Triângulo de Pascal: Definição e Construção

O triângulo de Pascal é a organização dos coeficientes binomiais em uma tabela. É infinito e formado por números binominais, iniciando a partir do 0 (zero).

Definição

O triângulo de Pascal são números organizados em uma tabela formada por números binomiais da seguinte forma:

Os números binomiais no triângulo são formados por

Onde:

• n: representa o número de linhas.
• k: representa o número de coluna.

O número n representa o “numerador” do número binomial e o número k representa o “denominador”.

Assim, temos a seguinte tabela com os números binomiais dispostos:

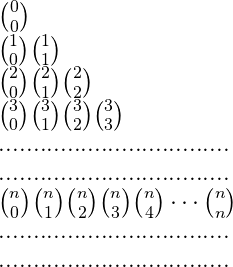
No triângulo acima, se os números binominais tiverem o mesmo “numerador”, então diz-se que eles estão na mesma linha do triângulo. Se os números tiverem o mesmo “denominador”, então diz-se que eles estão na mesma coluna do triângulo.

Substituindo os números binominais por cada valor correspondente, temos:

Coeficiente Binomial

Os números binomiais são representados por:

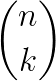
Onde:

• n: é chamado “numerador”
• k: é chamado “denominador”
• Com n ≥ k, e n e k são números naturais

Para calcular cada número binomial, utilizamos a seguinte expressão:

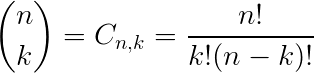
Onde:

• C_n,k: é uma combinação simples com n elementos tomados k a k.
• n!: é o fatorial de um número n qualquer.
• k! também é o fatorial de um número k qualquer.

O fatorial de um número é calculado da seguinte forma:

n! = n . (n-1) . (n-2) . … . 3 . 2 . 1

Exemplo:

Fatorial de 5: 5! = 5 . 4 . 3 . 2 . 1

Construção do Triângulo de Pascal

É bem fácil construí-lo, precisamos apenas lembrar que os numeradores ficam na mesma linha e os denominadores na mesma coluna. Então, temos:

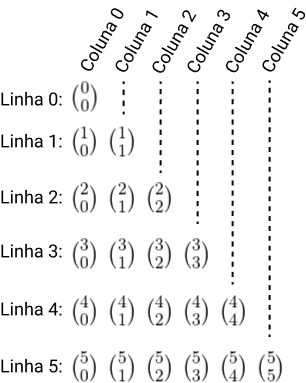
Pode seguir os seguintes passos na resolução dos números binomiais:

• Todos os elementos da coluna 0 é igual a 1.
• O último elemento de cada linha é igual a 1.
• O elemento que não está na coluna 0 e nem é o último elemento da linha, é a soma do número de cima mais o antecessor do número de cima.

Aplicando os passos acima, chegaremos ao seguinte resultado:

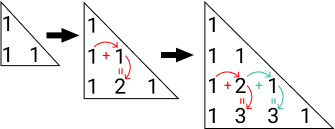
Propriedades

Relação de Stifel: um número no triângulo de Pascal é a soma do número de cima mais o antecessor desse mesmo número.

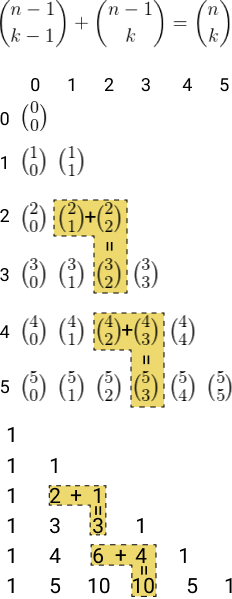
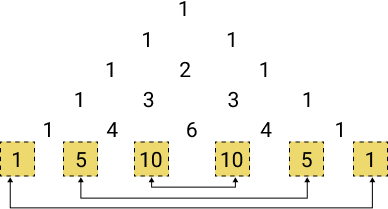
Simetria: o triângulo de Pascal é simétrico em relação à altura. Em uma linha qualquer, dois binomiais equidistantes dos extremos são iguais.

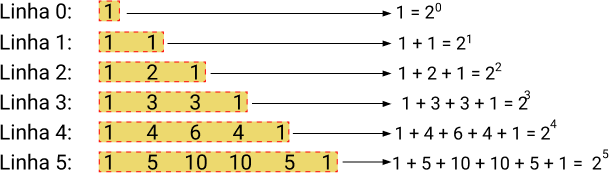
Teorema das Linhas: a soma de qualquer linha do triângulo de ordem n é igual a 2ⁿ.

Teorema das Colunas: a soma dos números binomiais de uma coluna no triângulo de Pascal, a partir do primeiro elemento, tem como resultado o número binomial à direita da linha abaixo do último elemento somado.

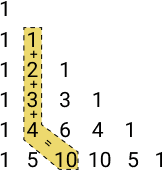
Teorema das Transversais: s soma dos números de uma diagonal qualquer do triângulo de Pascal, a partir do primeiro elemento da diagonal, é igual ao elemento abaixo do último elemento somando.

Binômio de Newton

O Binômio de Newton é uma potência da seguinte forma (x + y)ⁿ, com n ∈ R.

A fórmula geral do Binômio de Newton para o expoente n é a seguinte:

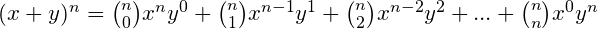
Os coeficientes do binômio correspondem aos números binomiais do triângulo de Pascal.

Exemplo:

Vamos desenvolver o seguinte binômio: (x + 2)³.

1 . x³ . 2⁰ + 3 . x² . 2¹ + 3 . x¹ . 2² + 1 . x⁰ . 2³

Os números em negritos são os números correspondentes a 3ª linha do triângulo de Pascal, já que n = 3. Então, a 3ª linha do triângulo são: 1 3 3 1.

Resolvendo o binômio acima temos:

x³ + 6x² + 12x + 8

Que é uma equação de grau 3.

Para valores pequenos é tranquilo resolver um binômio. No entanto, para valores maiores torna-se muito complicado sua solução. Uma saída é recorrer ao triângulo de Pascal para determinar os coeficientes binomiais para a correta expansão do binômio.