As relações métricas no triângulo retângulo relacionam as medidas entre os elementos do triângulo.
O triângulo retângulo ABC a seguir apresenta os elementos principais:
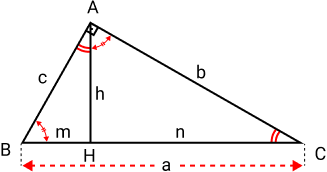
Onde:
- a: representa a hipotenusa;
- c e b: são os catetos;
- h: é a altura do triângulo em relação à hipotenusa;
- m e n: são, respectivamente, as projeções dos catetos c e b sobre a hipotenusa.
Triângulos Retângulos Semelhantes
Em qualquer triângulo retângulo, a altura relativa à hipotenusa divide o triângulo retângulo em dois triângulos, que também são retângulos. Sendo os dois triângulos semelhantes ao primeiro e semelhantes entre si.
Exemplo:
Seja o triângulo ABC com hipotenusa a e altura h:

Para o triângulo retângulo ABC acima, sendo BC = a, AC = b, AB = c, AH = h, BH = m, e CH = n, então as seguintes relações são válidas:
- Relações de Euclides:
- b² = a . n
- c² = a . m
-
Teorema de
Pitágoras:
-
a² = b² + c²
-
a² = b² + c²
- h² = m . n
- b . c = a . h
Os triângulos HCA e ACB são semelhantes entre si, obedecendo ao critério (AA~). Então:
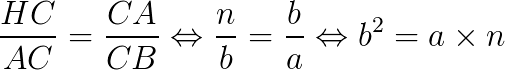
Os triângulos HBA e ABC também são semelhantes entre si, obedecendo ao critério (AA~). Então:
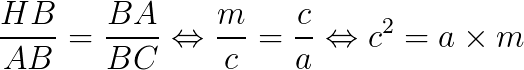
Se somarmos membro a membro as relações que mostramos acima, então chegamos no Teorema de Pitágoras:
an + am = b² + c² ⇔ a(n + m) = b² + c² ⇔ a . a = b² + c² ⇔ a² = b² + c²
Os triângulos HBA e HAC também são semelhantes pelo critério (AA~). Então, temos que:
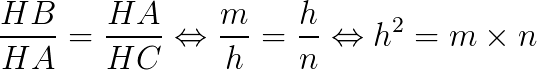
Os triângulos HBA e ABC são semelhantes entre si pelo critério (AA~). Então:
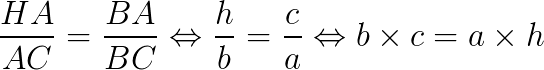
Estão são as principais relações métricas no triângulo retângulo, e importantes no cálculo de problemas.
Exercício Resolvido
Encontre o valor de x, y e z no
triângulo retângulo:
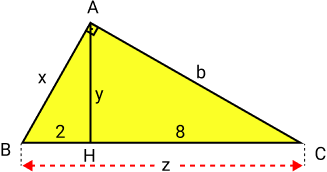
Resolução:
Cálculo do valor de z
- z = 8 + 2 = 10
Agora, para encontrarmos o valor de x vamos aplicar a relação: c² = a . m
- x² = 10 . 2 ⇒ x² = 20 ⇒ x = √20 = 2√5 = 4,47
Vamos calcular o valor de y aplicando a relação: h² = m . n
- y² = 8 . 2 ⇒ y² = 16 ⇒ y = √16 = 4
Exercícios propostos
Veja os exercícios no link a seguir:

