Treine seus conhecimentos sobre triângulo retângulo respondendo os exercícios envolvendo as relações métricas do triângulo retângulo.
1) Calcule a altura do triângulo.
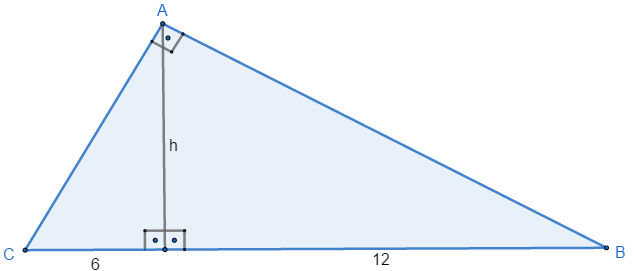
Ver resposta
A altura desse triângulo é dada pela relação h² = m . n
h² = m . n ⇒
h² = 12 . 6 ⇒
h = √72 = 8,485
2) Calcule a medida de x.
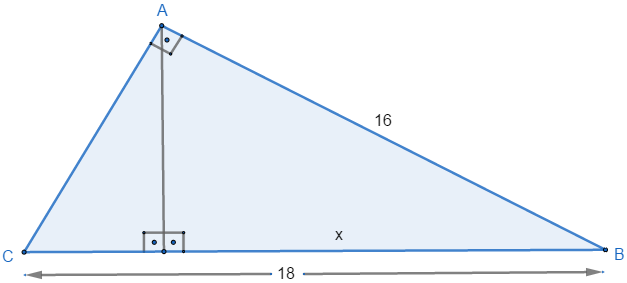
Ver resposta
Para calcular a medida de x, usamos a seguinte relação b² = a . m
b² = a . m ⇒
16² = 18 . x ⇒
256 = 18 . x ⇒
x = 256/18 ⇒
x = 14,22
3) Determine no triângulo abaixo a medida da hipotenusa, a altura em relação à hipotenusa e a projeção dos catetos sobre a hipotenusa.
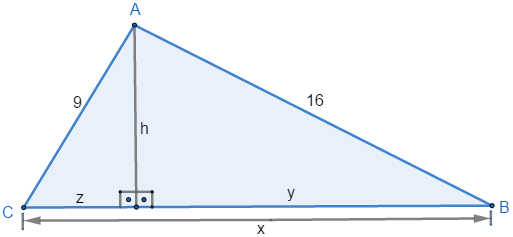
Ver resposta
Para o triângulo externo podemos determinar o valor de x através do teorema de Pitágoras.
Assim:
x² = 9² + 16² ⇒
x² = 81 + 256 ⇒
x = √337 ⇒
x = 18,36
Agora, as projeções dos catetos sobre a hipotenusa temos:
9² = x . z ⇒
81 = 18,36 . z ⇒
z = 81/18,36 ⇒
z = 4,4
16² = x . y ⇒
256 = 18,36 . y⇒
y = 256/18,36 ⇒
y = 13,9
Vamos determinar a altura h através da relação do produto entre os catetos.
Então:
x . h = 9 . 16 ⇒
18,36 . h = 144 ⇒
h = 144/18,36 ⇒
h = 7,8
As relações métricas no triângulo retângulo são ideais para resolver exercícios onde falta uma medida do lado do triângulo retângulo.


